OPICO 1: Algorithms for Item Sequence Generation
Part 1 in a series on: Optimization Problems with Items and Categories in Oracle
The knapsack problem is a problem in combinatorial optimization: Given a set of items, each with a weight and a value, determine the number of each item to include in a collection so that the total weight is less than or equal to a given limit and the total value is as large as possible.
The knapsack problem and many other problems in combinatorial optimization require the selection of a subset of items to maximize an objective function subject to constraints. A common approach to solving these problems algorithmically involves recursively generating sequences of items of increasing length in a search for the best subset that meets the constraints.
I applied this kind of approach using SQL for a number of problems, starting in January 2013 with A Simple SQL Solution for the Knapsack Problem (SKP-1), and I wrote a summary article, Knapsacks and Networks in SQL, in December 2017 when I put the code onto GitHub, sql_demos - Brendan’s repo for interesting SQL.
This is the first in a series of eight articles that aim to provide a more formal treatment of algorithms for item sequence generation and optimization, together with practical implementations, examples and verification techniques in SQL and PL/SQL.
List of Articles
- OPICO 1: Algorithms for Item Sequence Generation
- OPICO 2: SQL for Item Sequence Generation
- OPICO 3: Algorithms for Item/Category Optimization
- OPICO 4: Recursive SQL for Item/Category Optimization
- OPICO 5: Tuning Recursive SQL for Item/Category Optimization
- OPICO 6: Mixed SQL and PL/SQL Methods for Item/Category Optimization
- OPICO 7: Verification
- OPICO 8: Automation
GitHub 
- Optimization Problems with Items and Categories in Oracle
[See README for references]
Twitter 
In the current article we review methods for recursive generation of the item sequences in a generic way that is not specific to SQL or any programming language. We cover different types of item sequence, types of recursive search, breadth-first recursion for each sequence type, and choice of root set.
The discussion uses mathematical symbolism where appropriate, which allows for precise statements of the ways that the methods work, and allows us to verify easily that they do in fact generate all the desired sequences.

[Image by Gerd Altmann from Pixabay]
Contents
↓ 1 Item Sequence Types
↓ 2 Graph Traversal Search Types
↓ 3 Recursion Methods by Sequence Type
↓ 4 Root Sequence
↓ 5 Conclusion
1 Item Sequence Types
In general we assume that we have a set of n items with unique identifiers, from which we want to form sequences of r items. Here are some definitions from Wikipedia to help us classify the different types of sequence possible:
In mathematics, a set is a well-defined collection of distinct objects, considered as an object in its own right
...a multiset (aka bag or mset) is a modification of the concept of a set that, unlike a set, allows for multiple instances for each of its elements
The article mentions the well-known multiset example of the prime factors of an integer; for example, 120 = 2x2x2x3x5.
...a permutation of a set is, loosely speaking, an arrangement of its members into a sequence or linear order
...a combination is a selection of items from a collection, such that (unlike permutations) the order of selection does not matter
We can look for all sequences of r items from n, of four different types, based on the concepts above. The table below summarises the properties of the four types, with sequences listed for a small example of n=3, r=2, and the total numbers of sequences for a larger example size of n=100, r=10 (which I got from this handy page: Discrete Mathematics Calculators).

Let I denote a set of n items, and 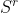 denote a set of sequences of length r of items from I. We can write
denote a set of sequences of length r of items from I. We can write 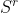 as a set of r-tuples, with an index j within the set:
as a set of r-tuples, with an index j within the set:
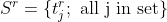
where 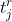 is the is the j’th r-tuple in the set.
is the is the j’th r-tuple in the set.
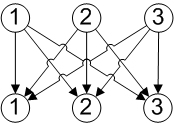
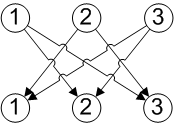
If we display the set of n items in a row and repeat the row r times, as an array of nodes, then the task of generating the sequences can be seen as equivalent to generating graphs by adding links between successive rows. For example, here is the array for the case of 3 items and sequence length 2:
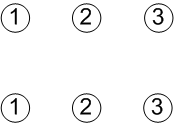
2 Graph Traversal Search Types
Breadth First Search (Wikipedia)
... starts at the tree root (or some arbitrary node of a graph, sometimes referred to as a 'search key'), and explores all of the neighbor nodes at the present depth prior to moving on to the nodes at the next depth level.
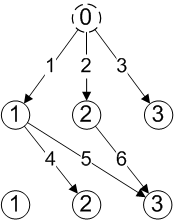
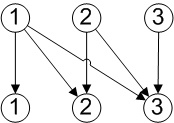
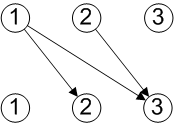
This diagram shows how the graph for distinct combinations of 2 items from 3 would be generated via breadth first search, with the arrow numbers showing traversal order, assuming we take items in numerical order. The node labelled ‘0’ is a dummy node allowing the first step to be represented by an arc.
Depth First Search (Wikipedia)
... starts at the root node (selecting some arbitrary node as the root node in the case of a graph) and explores as far as possible along each branch before backtracking.
This diagram shows how the graph for distinct combinations of 2 items from 3 would be generated via depth first search, with the arrow numbers showing traversal order.
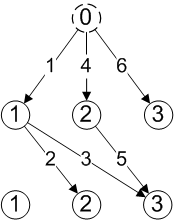
Notice that depth first searches tend to produce full length sequences earlier than with breadth first. In this example the second step leads to a full combination, whereas in the breadth first diagram we see that a full combination is first generated at the fourth step. Now we can show how to generate recursively all sequences of r items from a set of n, for each type of sequence. The recursions follow the breadth first search approach, which is what will be required when we implement algorithms in SQL.
3 Recursion Methods by Sequence Type
↑ Contents
↓ 3.1 MP: Multiset Permutation [Items may repeat, order matters]
↓ 3.2 MC: Multiset Combination [Items may repeat, order does not matter]
↓ 3.3 SP: Set Permutation [Items may not repeat, order matters]
↓ 3.4 SC: Set Combination [Items may not repeat, order does not matter]
3.1 MP: Multiset Permutation [Items may repeat, order matters]
↑ 3 Recursion Methods by Sequence Type
↓ Recursion
↓ Explanation
The number of sequences of type MP of size r from a set of n items = 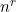
For example, when n = 3 and r = 2, the number of MP sequences is:
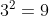
Here are the 9 multiset permutations of 2 items from 3: 11,12,13,21,22,23,31,32,33
There are 100,000,000,000,000,000,000 ways to choose 10 from 100 items in sequences of type MP.
Recursion
↑ 3.1 MP: Multiset Permutation [Items may repeat, order matters]
Suppose that 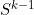 is the set of all sequences (or tuples, t) of length k-1 of items from I of type Multiset Permutation:
is the set of all sequences (or tuples, t) of length k-1 of items from I of type Multiset Permutation:
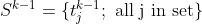
Then we can generate the set 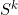 as the set of k-tuples:
as the set of k-tuples:
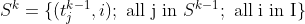
where  is the k-tuple constructed by adding item i onto the j’th (k-1)-tuple.
is the k-tuple constructed by adding item i onto the j’th (k-1)-tuple.
Explanation
↑ 3.1 MP: Multiset Permutation [Items may repeat, order matters]
If we have the set of all permutations of length k-1, then the set for length k is generated by adding an extra item to each sequence in turn, for each item.If we create a new sequence for each item for each existing sequence then we will have the full set for k items.
3.2 MC: Multiset Combination [Items may repeat, order does not matter]
↑ 3 Recursion Methods by Sequence Type
↓ Recursion
↓ Explanation
The number of sequences of type MC of size r from a set of n items is given by the number of combinations of r items from a set of (n+r-1) items, which, using the combinatorial formula for choosing r items from (n+r-1) is:
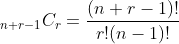
This is not so obvious, and is usually demonstrated by means of a Stars and bars diagram, in which the set items are represented as buckets delimited by n - 1 bars (‘|’), with r stars (‘*’) placed between the delimiters representing the multiplicity of that bucket, or item. Each distinct sequence is then represented by a choice of r positions for the stars from the n + r - 1 available.
For example, when n = 3 and r = 2, the number of MC sequences is:
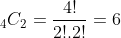
Here are the 6 multiset combinations of 2 items from 3, along with their stars and bars diagrams:
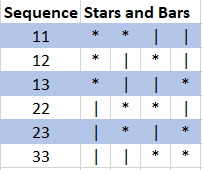
There are 42,634,215,112,710 ways to choose 10 from 100 items in sequences of type MC.
Recursion
↑ 3.2 MC: Multiset Combination [Items may repeat, order does not matter]
With combination types of sequence the order of items does not matter, and we only want to obtain one instance, so we can take the item combination to be the unique permutation that is in some given order (the ordering can be alphabetic, for example, based on the unique identifier, or any other well-defined ordering).
Suppose now that 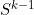 is the set of all sequences of length r-1 of items from I of type Multiset Combination, with each sequence arranged in increasing item order:
is the set of all sequences of length r-1 of items from I of type Multiset Combination, with each sequence arranged in increasing item order:
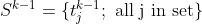
Then we can generate the set 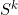 as the set of k-tuples:
as the set of k-tuples:
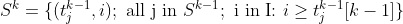
where  is the k-tuple constructed by adding item i onto the j’th (k-1)-tuple and
is the k-tuple constructed by adding item i onto the j’th (k-1)-tuple and  is the (k-1)’th item in the j’th (k-1)-tuple.
is the (k-1)’th item in the j’th (k-1)-tuple.
Explanation
↑ 3.2 MC: Multiset Combination [Items may repeat, order does not matter]
If we have the set of all combinations of length r-1 arranged with items in increasing order, then the set for length r is generated by adding an extra item to each sequence in turn, for each eligible item. An item is eligible for a given sequence if it is of order not less than the last item in the sequence, since the items are arranged in order.If we create a new sequence for each eligible item for each existing sequence then we will have the full set for r items, also arranged in order.
3.3 SP: Set Permutation [Items may not repeat, order matters]
↑ 3 Recursion Methods by Sequence Type
↓ Recursion
↓ Explanation
The number of sequences of type SP of size r from a set n items is given by the usual permutation formula:
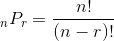
For example, when n = 3 and r = 2, the number of SP sequences is:
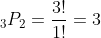
Here are the 6 set permutations of 2 items from 3: 12,13,21,23,31,32
There are 62,815,650,955,529,472,000 ways to choose 10 from 100 items in sequences of type SP.
Recursion
↑ 3.3 SP: Set Permutation [Items may not repeat, order matters]
Suppose now that 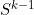 is the set of all sequences (or tuples, t) of length k-1 of items from I of type Set Permutation:
is the set of all sequences (or tuples, t) of length k-1 of items from I of type Set Permutation:
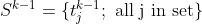
Then we can generate the set 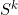 as the set of k-tuples:
as the set of k-tuples:
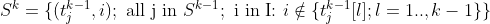
where  is the k-tuple constructed by adding item i onto the j’th (k-1)-tuple and
is the k-tuple constructed by adding item i onto the j’th (k-1)-tuple and 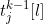 is the l’th item in the j’th (k-1)-tuple.
is the l’th item in the j’th (k-1)-tuple.
Explanation
↑ 3.3 SP: Set Permutation [Items may not repeat, order matters]
If we have the set of all permutations, without repeats, of length k-1, then the set for length k is generated by adding an extra item to each sequence in turn, for each eligible item. An item is eligible for a given sequence if it does not already appear in the sequence.If we create a new sequence for each eligible item for each existing sequence then we will have the full set for k items.
3.4 SC: Set Combination [Items may not repeat, order does not matter]
↑ 3 Recursion Methods by Sequence Type
↓ Recursion
↓ Explanation
The number of sequences of type SC of size r from a set n items is given by the usual combinations formula:
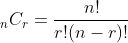
For example, when n = 3 and r = 2, the number of SC sequences is:
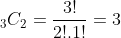
Here are the 3 combinations of 2 items from 3: 12,13,23
There are 17,310,309,456,440 ways to choose 10 from 100 items in sequences of type SC.
Recursion
↑ 3.4 SC: Set Combination [Items may not repeat, order does not matter]
Suppose now that 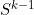 is the set of all sequences of length k-1 of items from I of type Set Combination, with each sequence arranged in increasing item order:
is the set of all sequences of length k-1 of items from I of type Set Combination, with each sequence arranged in increasing item order:
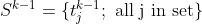
Then we can generate the set 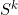 as the set of k-tuples:
as the set of k-tuples:
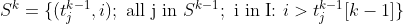
where  is the k-tuple constructed by adding item i onto the j’th (k-1)-tuple and
is the k-tuple constructed by adding item i onto the j’th (k-1)-tuple and  is the (k-1)’th item in the j’th (k-1)-tuple.
is the (k-1)’th item in the j’th (k-1)-tuple.
Explanation
↑ 3.4 SC: Set Combination [Items may not repeat, order does not matter]
If we have the set of all combinations, without repeats, of length k-1, then the set for length k is generated by adding an extra item to each sequence in turn, for each eligible item. An item is eligible for a given sequence if it is of order strictly greater than the last item in the sequence, since the items are arranged in order.If we create a new sequence for each eligible item for each existing sequence then we will have the full set for k items, also arranged in order.
4 Root Sequence
We showed above how to generate recursively the full set of sequences of length r from the set of length r-1, for each type of sequence. In order to anchor the recursion we need a root set for some r. In fact we can use the same root set for each type of sequence. The simplest choice is for r = 0, where the empty set matches all sequence types defined above. It’s also clear that the item set, I, also matches all definitions for r = 1. We can use either set as the root for the recursion for all four types of sequence.
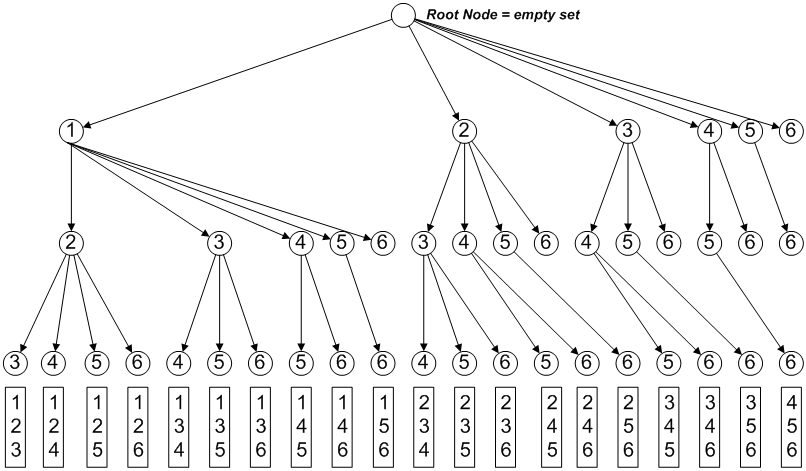
Example: 3 Item Set Combinations from 6
The diagram shows the recursion process for generating sequences of 3 items from 6 of type Set Combination as a tree diagram, starting from the empty set as root.
5 Conclusion
In this article we have shown in an abstract way how recursive techniques may be used to generate sequences of items that can form the basis of solutions for larger problems involving constraints and value optimization.
In the next article we will demonstrate how these algorithms can be implemented using recursive SQL. We will go on to demonstrate how PL/SQL can be used to implement both recursive and iterative versions with embedded SQL.
In the third article we will extend consideration beyond just the generation of sequences to optimization problems where we want to select sequences that maximize a value measure subject to constraints. This will follow a similarly mathematical approach for similar reasons.