OPICO 4: Recursive SQL for Item/Category Optimization
Part 4 in a series on: Optimization Problems with Items and Categories in Oracle
The knapsack problem is a problem in combinatorial optimization: Given a set of items, each with a weight and a value, determine the number of each item to include in a collection so that the total weight is less than or equal to a given limit and the total value is as large as possible.
The knapsack problem and many other problems in combinatorial optimization require the selection of a subset of items to maximize an objective function subject to constraints. A common approach to solving these problems algorithmically involves recursively generating sequences of items of increasing length in a search for the best subset that meets the constraints.
I applied this kind of approach using SQL for a number of problems, starting in January 2013 with A Simple SQL Solution for the Knapsack Problem (SKP-1), and I wrote a summary article, Knapsacks and Networks in SQL, in December 2017 when I put the code onto GitHub, sql_demos - Brendan’s repo for interesting SQL.
This is the fourth in a series of eight articles that aim to provide a more formal treatment of algorithms for item sequence generation and optimization, together with practical implementations, examples and verification techniques in SQL and PL/SQL.
List of Articles
- OPICO 1: Algorithms for Item Sequence Generation
- OPICO 2: SQL for Item Sequence Generation
- OPICO 3: Algorithms for Item/Category Optimization
- OPICO 4: Recursive SQL for Item/Category Optimization
- OPICO 5: Tuning Recursive SQL for Item/Category Optimization
- OPICO 6: Mixed SQL and PL/SQL Methods for Item/Category Optimization
- OPICO 7: Verification
- OPICO 8: Automation
GitHub 
- Optimization Problems with Items and Categories in Oracle
[See README for references]
Twitter 
In the third article, we extended the sequence generation algorithms of the first article to optimization problems where we want to select sequences that maximize a value measure subject to constraints. We showed in a generic way how one-level algorithms can be developed to eliminate infeasible, or suboptimal, paths as early as possible, and introduced Value Filtering techniques to allow for more efficient two-level algorithms.
In the current article, we go on to show how the one-level algorithms can be implemented using recursive SQL. Having used mathematical notation to describe the problems and algorithms in the third article, here we’ll take a more visual approach starting with a simple example to describe the problem.

[Image by Gerd Altmann from Pixabay]
Contents
↓ 1 Example Problem: Choose 3 Items from 6 with 2 Categories
↓ 2 Passing Bind Variables into Views
↓ 3 Solution by Post-Validation of Sequences
↓ 4 Solution by Preemptive Sequence Truncation
↓ 5 Conclusion
1 Example Problem: Choose 3 Items from 6 with 2 Categories
The example problem is a simple generic example with 6 items and 2 categories which we can illustrate with a couple of diagrams. First here is a diagram showing the items, with prices and values, and the categories with their constraints as well as the overall item number size constraint.

We can show all 20 combinations with associated price and value totals in the following diagram, setting a price limit of 5:
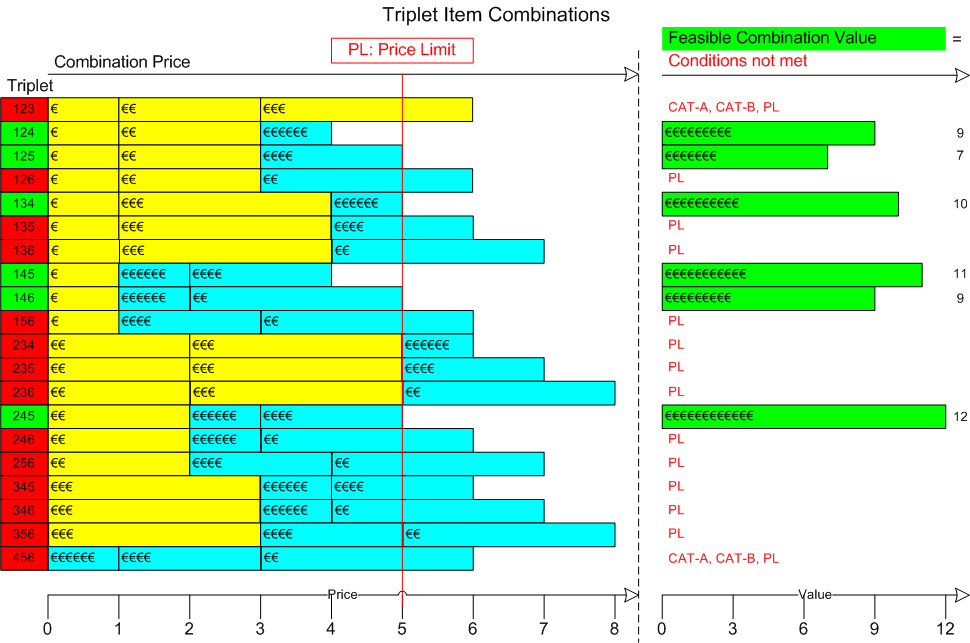
The general problem is to find the combinations of r items from a set of n that maximize value subject to a price limit, while meeting constraints on the numbers of items in each category.
If we look at the diagrams for the simple example above it’s easy to see which combinations are feasible and to pick out the ones with greatest value. For larger problems though, this is impractical, and we will develop some SQL techniques to solve the problem. The most obvious approach is to use our sequence generation code to generate all sequences (of set combination type) of the right length, then eliminate those that violate constraints. However, we saw in the first article that the numbers of combinations quickly become extremely large as the numbers of items increases (for example, there are 17,310,309,456,440 combinations of 10 items from 100). Therefore we’ll need to be a bit smarter, to eliminate combinations as we go with logic, using the techniques developed in a generic way in the third article, this time in SQL.
It is nonetheless worth developing the SQL for the more obvious approach first, as the SQL itself involves some interesting features, and we can certainly solve our simple example problem in this way.
2 Passing Bind Variables into Views
In sqlplus (and other SQL front ends), SQL statements can be parameterized using bind variables, and we use this approach in the script best_combis_post_valid.sql. For example, the maximum price uses a bind variable defined as:
VAR MAX_PRICE NUMBER
and set like this:
BEGIN
:MAX_PRICE := 5;
END;
/
and used like this:
AND tot_price <= :MAX_PRICE
Views in Oracle cannot be directly parameterized, but there are indirect ways of passing in parameters. We will use the system contexts method in which session level variables can be set through calls to a packaged procedure, and then referenced in SQL. Here’a an Oracle-Base article on creating and using these contexts in dynamic SQL: Dynamic Binds Using Contexts. The creation and setting is the same for use with views, and here is the code we are using:
Grant Create Any Context to user (from admin user)
GRANT CREATE ANY CONTEXT TO &LIB_USER;
Create the context
This creates the context specifying the package name Item_Cat_Seqs for the package that can set the context values:
CREATE OR REPLACE CONTEXT Recursion_Ctx USING Item_Cat_Seqs;
Set the context variable
DBMS_Session.Set_Context('RECURSION_CTX', p_ctx_name, p_ctx_value);
Reference the context variable
We reference the context as follows, where a context named ‘RECURSION_CTX’ has been created, with a variable ‘MAX_PRICE’, and the following is an item in the Select list:
To_Number(SYS_Context('RECURSION_CTX', 'MAX_PRICE')) max_price,
It’s worth noting here that context variables may behave slightly differently from straight bind variables in terms of query processing, in that bind variable peeking does not occur (Oracle v19.3), as demonstrated by Connor McDonald here: Taking a peek at SYS_CONTEXT. As Connor notes, whether this is a good or a bad thing varies, and in our case it is not important.
3 Solution by Post-Validation of Sequences
↑ Contents
↓ Post-Validation SQL Components
↓ View for Best Item Combinations via Post-Validation Method
↓ Subquery Structure
In this section we show how to solve the optimization problem in SQL by obtaining all combinations, eliminating the infeasible ones, then ranking them: An approach that is only possible for very small problems. We start by discussing the SQL components, then show a view for the solutions at path level, and explain the the subqueries.
Post-Validation SQL Components
↑ 3 Solution by Post-Validation of Sequences
↓ Splitting Path into Items
↓ Getting All Combinations
↓ Getting All Feasible Combinations
Splitting Path into Items
↑ Post-Validation SQL Components
The query in the second article for generating sequences of type SC (Set/Combination) generates the combinations as paths containing the sequences of item ids. Assuming that the item ids are strings of fixed width, we can easily split out the items into separate records. To do this we use a row-generator subquery to generate the integers from 1 to r (here 3) as item index, cross-join this subquery with the record set, and use the item index in a substring expression to extract the item ids. The snippet from the joins section is:
CROSS JOIN (SELECT LEVEL item_index FROM DUAL CONNECT BY LEVEL <= :SEQ_SIZE) ind
JOIN items itm
ON itm.id = To_Number(Substr (trw.path, (ind.item_index - 1) * :ITEM_WIDTH + 1, :ITEM_WIDTH))
Getting All Combinations
↑ Post-Validation SQL Components
↓ Query
↓ Result for Example
Here is a query to get all the combinations:
Query
WITH tree_walk(item_id, lev, tot_price, tot_value, cat_id, path) AS (
SELECT '0', 0, 0, 0, CAST (NULL AS VARCHAR2(400)), CAST (NULL AS VARCHAR2(400))
FROM DUAL
UNION ALL
SELECT itm.id,
trw.lev + 1,
trw.tot_price + itm.item_price,
trw.tot_value + itm.item_value,
itm.category_id,
trw.path || itm.id
FROM tree_walk trw
JOIN items itm
ON itm.id > trw.item_id
WHERE trw.lev < :SEQ_SIZE
)
SELECT trw.path,
trw.tot_price,
trw.tot_value,
itm.category_id,
itm.id item_id,
itm.item_price,
itm.item_value
FROM tree_walk trw
CROSS JOIN (SELECT LEVEL item_index FROM DUAL CONNECT BY LEVEL <= :SEQ_SIZE) ind
JOIN items itm
ON itm.id = To_Number(Substr (trw.path, (ind.item_index - 1) * :ITEM_WIDTH + 1, :ITEM_WIDTH))
WHERE trw.lev = :SEQ_SIZE
ORDER BY trw.path, itm.id
Result for Example
For our example problem, with r = 3 and n = 6, the result is:
Path Total Price Total Value Category Item Item Price Item Value
---- ----------- ----------- -------- ---- ---------- ----------
123 6 6 CAT_1 1 1 1
2 2 2
3 3 3
124 4 9 CAT_1 1 1 1
2 2 2
CAT_2 4 1 6
125 5 7 CAT_1 1 1 1
2 2 2
CAT_2 5 2 4
126 6 5 CAT_1 1 1 1
2 2 2
CAT_2 6 3 2
134 5 10 CAT_1 1 1 1
3 3 3
CAT_2 4 1 6
135 6 8 CAT_1 1 1 1
3 3 3
CAT_2 5 2 4
136 7 6 CAT_1 1 1 1
3 3 3
CAT_2 6 3 2
145 4 11 CAT_1 1 1 1
CAT_2 4 1 6
5 2 4
146 5 9 CAT_1 1 1 1
CAT_2 4 1 6
6 3 2
156 6 7 CAT_1 1 1 1
CAT_2 5 2 4
6 3 2
234 6 11 CAT_1 2 2 2
3 3 3
CAT_2 4 1 6
235 7 9 CAT_1 2 2 2
3 3 3
CAT_2 5 2 4
236 8 7 CAT_1 2 2 2
3 3 3
CAT_2 6 3 2
245 5 12 CAT_1 2 2 2
CAT_2 4 1 6
5 2 4
246 6 10 CAT_1 2 2 2
CAT_2 4 1 6
6 3 2
256 7 8 CAT_1 2 2 2
CAT_2 5 2 4
6 3 2
345 6 13 CAT_1 3 3 3
CAT_2 4 1 6
5 2 4
346 7 11 CAT_1 3 3 3
CAT_2 4 1 6
6 3 2
356 8 9 CAT_1 3 3 3
CAT_2 5 2 4
6 3 2
456 6 12 CAT_2 4 1 6
5 2 4
6 3 2
60 rows selected.
Getting All Feasible Combinations
↑ Post-Validation SQL Components
↓ Price and Category Constraints
↓ Query
↓ Result for Example
Now, having the code to generate all combinations of the correct size, we can obtain the feasible combinations, i.e. those that match the additional price and category constraints, and sort them in order of total value. To do this, we use the query above that splits the items into separate records, and use it as a subquery in another subquery where the additional constraints are applied.
Price and Category Constraints
↑ Getting All Feasible Combinations
The price constraint is straightforward:
psp.tot_price <= :MAX_PRICE
The category constraints are a bit trickier. We need to join the categories table with the items to get the minimum and maximum counts, and check which paths satisfy them. However, not all paths may have items in each category and we need to check all category constraints for each path. This means we need to drive from the categories table and outer join the item-path records. However, a standard outer join is insufficent because the outer join only ensures that a single record is returned for each category if no paths are joined. What we need is for each category/path pair to be returned with the category fields and path identifier even if no path has an item in that category. This can be achieved with a partitioned outer join, in which we put the partition clause after the outer join clause, like this:
LEFT JOIN path_split psp PARTITION BY (psp.path)
[You can learn more about data densification techniques here: Oracle Database Data Warehousing Guide - Data Densification for Reporting - v19.3]
We need to identify paths for which the item count in each category is within the category limits, and in practice it’s simpler to identify all the category/path pairs that do not match the condition. To do this, we group by path and category and apply the minimum/maximum constraints against counts of items. We need to be careful to count only records with not null item fields, since the partitioned outer join will return a path record padded with nulls for categories not present on a path, so for example, COUNT(psp.item_id), rather than COUNT(*). A HAVING clause is applied to select only category/path records that do not match the category condition. This gives us a list of infeasible paths which we can use to filter in a subsequent subquery. The infeasible_paths subquery is:
SELECT psp.path
FROM categories cat
LEFT JOIN path_split psp PARTITION BY (psp.path)
ON psp.category_id = cat.id
WHERE cat.id != 'AL'
GROUP BY psp.path,
cat.id,
cat.min_items,
cat.max_items
HAVING NOT COUNT(psp.item_id) BETWEEN cat.min_items AND cat.max_items
Now, with all the building blocks in place, we can obtain the full query. This selects from the earlier subquery for paths and items, uses the query above as a subquery to identify, and exclude, the infeasible paths, then orders the results by total value and price.
Query
↑ Getting All Feasible Combinations
WITH tree_walk(item_id, lev, tot_price, tot_value, cat_id, path) AS (
SELECT '0', 0, 0, 0, CAST (NULL AS VARCHAR2(400)), CAST (NULL AS VARCHAR2(400))
FROM DUAL
UNION ALL
SELECT itm.id,
trw.lev + 1,
trw.tot_price + itm.item_price,
trw.tot_value + itm.item_value,
itm.category_id,
trw.path || itm.id
FROM tree_walk trw
JOIN items itm
ON itm.id > trw.item_id
WHERE trw.lev < :SEQ_SIZE
), path_split AS (
SELECT trw.path,
trw.tot_price,
trw.tot_value,
To_Number(Substr (trw.path, (ind.item_index - 1) * :ITEM_WIDTH + 1, :ITEM_WIDTH)) item_index,
itm.category_id,
itm.id item_id,
itm.item_price,
itm.item_value
FROM tree_walk trw
CROSS JOIN (SELECT LEVEL item_index FROM DUAL CONNECT BY LEVEL <= :SEQ_SIZE) ind
JOIN items itm
ON itm.id = To_Number(Substr (trw.path, (ind.item_index - 1) * :ITEM_WIDTH + 1, :ITEM_WIDTH))
WHERE trw.lev = :SEQ_SIZE
), infeasible_paths AS (
SELECT psp.path
FROM categories cat
LEFT JOIN path_split psp PARTITION BY (psp.path)
ON psp.category_id = cat.id
AND psp.tot_price <= :MAX_PRICE
WHERE cat.id != 'AL'
GROUP BY psp.path,
cat.id,
cat.min_items,
cat.max_items
HAVING NOT COUNT(psp.item_id) BETWEEN cat.min_items AND cat.max_items
)
SELECT path,
tot_value,
tot_price,
category_id,
item_id,
item_value,
item_price
FROM path_split
WHERE path NOT IN (SELECT fpa.path FROM infeasible_paths fpa)
ORDER BY tot_value DESC, tot_price, path, item_id
Result for Example
↑ Getting All Feasible Combinations
For our example problem, with r = 3 and n = 6, the result is:
Path Total Value Total Price Category Item Item Value Item Price
---- ----------- ----------- -------- ---- ---------- ----------
245 12 5 CAT_1 2 2 2
CAT_2 4 6 1
5 4 2
145 11 4 CAT_1 1 1 1
CAT_2 4 6 1
5 4 2
134 10 5 CAT_1 1 1 1
3 3 3
CAT_2 4 6 1
124 9 4 CAT_1 1 1 1
2 2 2
CAT_2 4 6 1
146 9 5 CAT_1 1 1 1
CAT_2 4 6 1
6 2 3
125 7 5 CAT_1 1 1 1
2 2 2
CAT_2 5 4 2
View for Best Item Combinations via Post-Validation Method
↑ 3 Solution by Post-Validation of Sequences
↓ View - RSF_POST_VALID_V
↓ Query Structure Diagram
↓ Result
We are going to unit test the SQL for the solution using this post-validation method, along with several other solution methods, and for this purpose it is convenient to create views. It will be simpler to test versions of the SQL that return records at item path level rather than item level, with columns for:
- Path
- Total Value
- Total Price
- Rank
The view code is as follows:
View - RSF_POST_VALID_V
↑ View for Best Item Combinations via Post-Validation Method
WITH binds AS (
SELECT To_Number(SYS_Context('RECURSION_CTX', 'SEQ_SIZE')) seq_size,
To_Number(SYS_Context('RECURSION_CTX', 'MAX_PRICE')) max_price,
To_Number(SYS_Context('RECURSION_CTX', 'ITEM_WIDTH')) item_width
FROM DUAL
), tree_walk(item_id, lev, tot_price, tot_value, cat_id, path) AS (
SELECT '0', 0, 0, 0, CAST (NULL AS VARCHAR2(400)), CAST (NULL AS VARCHAR2(400))
FROM DUAL
UNION ALL
SELECT itm.id,
trw.lev + 1,
trw.tot_price + itm.item_price,
trw.tot_value + itm.item_value,
itm.category_id,
trw.path || itm.id
FROM tree_walk trw
JOIN items itm
ON itm.id > trw.item_id
WHERE trw.lev < To_Number(SYS_Context('RECURSION_CTX', 'SEQ_SIZE'))
), path_split AS (
SELECT trw.path,
trw.tot_value,
trw.tot_price,
itm.category_id,
itm.id item_id
FROM tree_walk trw
CROSS JOIN binds bin
CROSS APPLY (SELECT LEVEL item_index FROM DUAL CONNECT BY LEVEL <= bin.seq_size) ind
JOIN items itm
ON itm.id = Substr (trw.path, (ind.item_index - 1) * bin.item_width + 1, bin.item_width)
WHERE trw.lev = bin.seq_size
), infeasible_paths AS (
SELECT psp.path
FROM categories cat
LEFT JOIN path_split psp PARTITION BY (psp.path)
ON psp.category_id = cat.id
WHERE cat.id != 'AL'
GROUP BY psp.path,
cat.id,
cat.min_items,
cat.max_items
HAVING NOT COUNT(psp.item_id) BETWEEN cat.min_items AND cat.max_items
)
SELECT path,
tot_value,
tot_price,
Row_Number() OVER (ORDER BY tot_value DESC, tot_price) rnk
FROM tree_walk trw
CROSS JOIN binds bin
WHERE trw.path NOT IN (SELECT fpa.path FROM infeasible_paths fpa)
AND trw.lev = bin.seq_size
AND trw.tot_price <= bin.max_price
Query Structure Diagram
↑ View for Best Item Combinations via Post-Validation Method

Result
↑ View for Best Item Combinations via Post-Validation Method
Path Total Value Total Price Rank
---- ----------- ----------- ----
245 12 5 1
145 11 4 2
134 10 5 3
124 9 4 4
146 9 5 5
125 7 5 6
6 rows selected.
Subquery Structure
↑ 3 Solution by Post-Validation of Sequences
Tree Walk
This has the recursive subquery factor that generates all item combinations of type SC (Set/Combination) as path strings. The anchor branch has a dummy item and null path. The recursive branch has a join condition othat ensures no duplicates are returned, and a termination condition using the SEQ_SIZE bind variable, read in via a system context.
Binds
This subquery reads in the bind variables from system context, and is present simply to reduce the boilerplate code associated with repeated calls to the context.
Paths Split
This subquery splits the path strings into individual items, using a row generator that joins SEQ_SIZE rows to each path record with an index used to pick out the particular item id from the path. The item fields along with path level fields are then selected for use in thhe next subquery.
Infeasible Paths
This subquery uses a partitioned outer join, as previously discussed, along with aggregation by path and category to identify all categories that have paths with invalid item category counts. Bind variables are read as columns from the Binds subquery.
Main (Item Paths) Subquery
The main subquery reads the paths of full length from the Tree Walk subquery, excludes any that are in the Infeasible Paths list, or that exceed the maximum price, and calculates the rank in descending order of value and ascending order of price, with bind variables read as columns from the Binds subquery.
4 Solution by Preemptive Sequence Truncation
↑ Contents
↓ View - RSF_SQL_V
↓ Query Structure Diagram
↓ Subquery Structure
In this section we show how to solve the optimization problem in SQL by preemptive sequence truncation, following the ideas set out generically in the third article: This approach, including the Value Bounding techniques, can be used for larger problems, as we’ll see in the next article.
We start by showing the path-level view, with a query structure diagram, then explain the subqueries in detail with cross-references to the conditions set out symbolically in the third article.
View - RSF_SQL_V
↑ 4 Solution by Preemptive Sequence Truncation
WITH item_rsums AS (
SELECT Row_Number() OVER (ORDER BY item_value DESC, id) index_value,
Sum(item_value) OVER (ORDER BY item_value DESC, id) sum_value,
Row_Number() OVER (ORDER BY item_price, id) index_price,
Sum(item_price) OVER (ORDER BY item_price, id) sum_price
FROM items
), category_rsums AS (
SELECT id, min_items, max_items,
Sum(CASE WHEN id != 'AL' THEN min_items END)
OVER (ORDER BY CASE WHEN min_items > 0 THEN max_items - min_items END DESC,
min_items,
max_items DESC,
id DESC) min_remain,
Lead(CASE WHEN min_items > 0 THEN id END)
OVER (ORDER BY CASE WHEN min_items > 0 THEN max_items - min_items END,
min_items DESC,
max_items,
id) next_cat,
Row_Number()
OVER (ORDER BY CASE WHEN min_items > 0 THEN max_items - min_items END,
min_items DESC,
max_items,
id) cat_rnk
FROM categories
), items_ranked AS (
SELECT itm.id item_id,
itm.category_id,
itm.item_price,
itm.item_value,
crs.min_items,
crs.max_items,
crs.min_remain,
crs.next_cat,
Row_Number() OVER (ORDER BY crs.cat_rnk, itm.item_value DESC, itm.id) item_rnk,
Count(*) OVER () n_items,
To_Number(SYS_Context('RECURSION_CTX', 'SEQ_SIZE')) seq_size,
To_Number(SYS_Context('RECURSION_CTX', 'MAX_PRICE')) max_price,
To_Number(Nvl(SYS_Context('RECURSION_CTX', 'MIN_VALUE'), '0')) min_value,
To_Number(Nvl(SYS_Context('RECURSION_CTX', 'KEEP_NUM'), '0')) keep_num
FROM items itm
JOIN category_rsums crs
ON crs.id = itm.category_id
), tree_walk(path_rnk, item_rnk, lev, tot_price, tot_value, cat_id, next_cat, same_cats, min_items, cats_path, path) AS (
SELECT 0, 0, 0, 0, 0, id, next_cat, 0, 0, CAST (NULL AS VARCHAR2(400)), CAST (NULL AS VARCHAR2(400))
FROM category_rsums
WHERE id = 'AL'
UNION ALL
SELECT Row_Number() OVER (PARTITION BY trw.cats_path || irk.category_id ORDER BY trw.tot_value + irk.item_value DESC),
irk.item_rnk,
trw.lev + 1,
trw.tot_price + irk.item_price,
trw.tot_value + irk.item_value,
irk.category_id,
irk.next_cat,
CASE irk.category_id WHEN trw.cat_id THEN trw.same_cats + 1 ELSE 1 END,
irk.min_items,
trw.cats_path || irk.category_id,
trw.path || irk.item_id
FROM tree_walk trw
JOIN items_ranked irk
ON irk.item_rnk BETWEEN (trw.item_rnk + 1) AND (irk.n_items - (irk.seq_size - trw.lev - 1))
LEFT JOIN item_rsums ivr
ON ivr.index_value = (irk.seq_size - trw.lev - 1)
LEFT JOIN item_rsums ipr
ON ipr.index_price = (irk.seq_size - trw.lev - 1)
WHERE trw.tot_price + irk.item_price + Nvl(ipr.sum_price, 0) <= irk.max_price
AND trw.tot_value + irk.item_value + Nvl(ivr.sum_value, 0) >= irk.min_value
AND (trw.path_rnk <= irk.keep_num OR irk.keep_num = 0)
AND trw.lev < irk.seq_size
AND CASE irk.category_id WHEN trw.cat_id THEN trw.same_cats + 1 ELSE 1 END <= irk.max_items
AND irk.seq_size - (trw.lev + 1) + Least(CASE irk.category_id
WHEN trw.cat_id THEN trw.same_cats + 1 ELSE 1 END,
irk.min_items)
>= irk.min_remain
AND (irk.category_id = trw.cat_id OR trw.same_cats >= trw.min_items)
AND (irk.category_id = trw.cat_id OR irk.category_id = Nvl(trw.next_cat, irk.category_id))
)
SELECT path,
tot_value,
tot_price,
Row_Number() OVER (ORDER BY tot_value DESC, tot_price) rnk
FROM tree_walk
WHERE lev = To_Number(SYS_Context('RECURSION_CTX', 'SEQ_SIZE'))
Query Structure Diagram
↑ 4 Solution by Preemptive Sequence Truncation

Subquery Structure
↑ 4 Solution by Preemptive Sequence Truncation
↓ Item Running Sums
↓ Value Running Sums
↓ Price Running Sums
↓ Category Running Sums
↓ Items Ranked
↓ Tree Walk
↓ Main (Item Paths) Subquery
Item Running Sums
This subquery computes the running sums of item values in descending order and of item prices in ascending order with index columns for the ranks in the lists. It is used to establish upper bounds on the total value, and lower bounds on the total price, at a given subsequence length, for the items that would complete the sequence. These bounds are then used to truncate paths where we deduce that they can’t lead to full sequences that are both within the price limit and of value at least equal to an input minimum. We show the subquery below, with a few extra columns for clarity, then query for value and price running sums separately.
WITH item_rsums AS (
SELECT id item_id, Row_Number() OVER (ORDER BY item_value DESC, id) index_value,
item_value,
Sum(item_value) OVER (ORDER BY item_value DESC, id) sum_value,
Row_Number() OVER (ORDER BY item_price, id) index_price,
item_price,
Sum(item_price) OVER (ORDER BY item_price, id) sum_price
FROM items
)
Value Running Sums
WITH item_rsums AS ...
SELECT index_value,
item_id,
item_value,
sum_value
FROM item_rsums
ORDER BY 1
Index Value Item Item Value Sum Value
------------ ---- ---------- -----------
1 4 6 6
2 5 4 10
3 3 3 13
4 2 2 15
5 6 2 17
6 1 1 18
Price Running Sums
WITH item_rsums AS ...
SELECT index_price,
item_id,
item_price,
sum_price
FROM item_rsums
ORDER BY 1
Index Price Item Item Price Sum Price
------------ ---- ---------- -----------
1 1 1 1
2 4 1 2
3 2 2 4
4 5 2 6
5 3 3 9
6 6 3 12
Category Running Sums
This subquery ranks the categories, provides a next category for the current category if the next ranked category has non-zero minimum items, and computes the sum of the minimum items over the remaining categories in rank order inclusive.
- The categories table contains a record with id ‘AL’, which is used as a source for the anchor branch of the tree walk subquery, and this is ranked first
- Categories with zero minimum items come after the non-zero ones
- Subject to the first two conditions, the ranking is designed to take the more restrictive categories first
- If min_items > 0 Then max_items - min_items Else Null (hence ordered last) - ‘AL’ record has zero
- min_items DESC - ‘AL’ record has largest value
- max_items
- id (tie-breaker)
- This ranking is used within the analytic Lead for next category, nulling if zero minimum items, and Row_Number for the rank
- The ranking is used in reverse for the running sum of minimum items remaining
SELECT id category_id, min_items, max_items,
Sum(CASE WHEN id != 'AL' THEN min_items END)
OVER (ORDER BY CASE WHEN min_items > 0 THEN max_items - min_items END DESC,
min_items,
max_items DESC,
id DESC) min_remain,
Lead(CASE WHEN min_items > 0 THEN id END)
OVER (ORDER BY CASE WHEN min_items > 0 THEN max_items - min_items END,
min_items DESC,
max_items,
id) next_cat,
Row_Number()
OVER (ORDER BY CASE WHEN min_items > 0 THEN max_items - min_items END,
min_items DESC,
max_items,
id) cat_rnk
FROM categories
ORDER BY CASE WHEN min_items > 0 THEN max_items - min_items END,
min_items DESC,
max_items,
id
Category Min Items Max Items Min Remaining Next Cat Rank
-------- ----------- ----------- -------------- -------- -----
AL 3 3 2 CAT_1 1
CAT_1 1 2 2 CAT_2 2
CAT_2 1 2 1 3
Items Ranked
This subquery ranks the items to provide an order in which they will be added in the tree walk. It’s essential that the first column in the rank order is the category rank as determined by the category_rsums query, and after that it seems sensible to look first at higher value items, with the item id as a tie-breaker. The subquery selects the item fields, and for convenience, also gets the value of the system context bind variables and counts the number of items.
WITH category_rsums AS ...(see above)
SELECT itm.id item_id,
itm.category_id,
itm.item_price,
itm.item_value,
Row_Number() OVER (ORDER BY crs.cat_rnk, itm.item_value DESC, itm.id) item_rnk,
Count(*) OVER () n_items,
To_Number(SYS_Context('RECURSION_CTX', 'SEQ_SIZE')) seq_size,
To_Number(SYS_Context('RECURSION_CTX', 'MAX_PRICE')) max_price,
To_Number(Nvl(SYS_Context('RECURSION_CTX', 'MIN_VALUE'), '0')) min_value,
To_Number(Nvl(SYS_Context('RECURSION_CTX', 'KEEP_NUM'), '0')) keep_num
FROM items itm
JOIN category_rsums crs
ON crs.id = itm.category_id
ORDER BY 5
Item Category Item Price Item Value ITEM_RNK N_ITEMS SEQ_SIZE MAX_PRICE MIN_VALUE KEEP_NUM
---- -------- ---------- ---------- ---------- ---------- ---------- ---------- ---------- ----------
3 CAT_1 3 3 1 6 3 5 10 10
2 2 2 2 6 3 5 10 10
1 1 1 3 6 3 5 10 10
4 CAT_2 1 6 4 6 3 5 10 10
5 2 4 5 6 3 5 10 10
6 3 2 6 6 3 5 10 10
Tree Walk
↑ Subquery Structure
↓ Join Conditions
↓ Where Conditions
This has the recursive subquery factor that generates item combinations of type SC (Set/Combination) as path strings. The anchor branch has a dummy item and null path. The recursive branch has a join condition othat ensures no duplicates are returned, and a termination condition using the SEQ_SIZE bind variable, read in via a system context. The recursive branch of the subquery joins the prior subqueries and uses them to apply additional conditions derived symbolically in the previous article in this series.
These conditions allow subsequences to be discarded early when we know they will lead to full length sequences that either do not meet the constraints, or that cannot be in the optimal set.
There are two additional conditions that implement the Value Filtering techniques explained in the third article (Minimum Value and Maximum Category-Rank below), in order to improve performance.
Join Conditions
↑ Tree Walk
The bracketed number [3.2.x] below is the label for the corresponding condition in the previous article.
- Items Ranked
JOIN items_ranked irk ON irk.item_rnk BETWEEN (trw.item_rnk + 1) AND (irk.n_items - (irk.seq_size - trw.lev - 1))Take items in rank order, and require enough slots left to complete sequence [3.2.2]
- Item Running Sums (Value)
LEFT JOIN item_rsums ivr ON ivr.index_value = (irk.seq_size - trw.lev - 1)Index is # slots left to fill after current one, to get sum_value, the maximum possible value sum from them [3.2.10]
- Item Running Sums (Price)
LEFT JOIN item_rsums ipr ON ipr.index_price = (irk.seq_size - trw.lev - 1)Index is # slots left to fill after current one, to get sum_price, the minimum possible price sum from them [3.2.3]
Where Conditions
- Maximum Price
WHERE trw.tot_price + irk.item_price + Nvl(ipr.sum_price, 0) <= irk.max_pricePrice sum, current + minimum possible from remaining slots <= maximum price [3.2.3]
- Minimum Value
AND trw.tot_value + irk.item_value + Nvl(ivr.sum_value, 0) >= irk.min_valueValue sum, current + maximum possible from remaining slots >= minimum value [3.2.10]. If minimum is zero, the condition is nullified
- Maximum Category-Rank
AND (trw.path_rnk <= irk.keep_num OR irk.keep_num = 0)Take only keep_num top-ranked (by category multiset) paths from prior iteration (if condition active) [3.2.9]. If keep_num is zero, the condition is nullified
- Sequence Length
AND trw.lev < irk.seq_sizeTermination condition on sequence length
- Category Maximum
AND CASE irk.category_id WHEN trw.cat_id THEN trw.same_cats + 1 ELSE 1 END <= irk.max_itemsNumber of items in current category <= maximum for that category [3.2.5]
- Category Minimum
AND irk.seq_size - (trw.lev + 1) + Least(CASE irk.category_id WHEN trw.cat_id THEN trw.same_cats + 1 ELSE 1 END, irk.min_items) >= irk.min_remainNumber of slots left + smaller of (current category count, min for current category) >= sum of count mins for remaining categories [3.2.6]
- Category Change - only when minimum met
AND (irk.category_id = trw.cat_id OR trw.same_cats >= trw.min_items)New category same as prior, or prior category minimum already met [3.2.7]
- Category Change - only to next ranked, unless zero minimum
AND (irk.category_id = trw.cat_id OR irk.category_id = Nvl(trw.next_cat, irk.category_id))Next category same as that of prior item, or is next ranked category, or: next ranked category has zero count minimum [3.2.8]
Main (Item Paths) Subquery
The main subquery reads the paths of full length from the Tree Walk subquery, with a rank calculated first by descending order of value, then by increasing price.
SELECT path,
tot_value,
tot_price,
Row_Number() OVER (ORDER BY tot_value DESC, tot_price) rnk
FROM tree_walk
WHERE lev = To_Number(SYS_Context('RECURSION_CTX', 'SEQ_SIZE'))
5 Conclusion
In this article, we explained how to use recursive SQL to solve the problem of optimizing a value function subject to constraints on item measures and on item categories, by implementing the algorithms described generically in the third.
In the next article we will introduce test problems of realistic size, and tune performance using techniques including hints and the use of temporary tables to pre-calculate values, with the Value Filtering techniques proving essential.
In the sixth article we will demonstrate how PL/SQL can be used to implement both recursive and iterative versions of the one-level algorithms with embedded SQL, and we’ll go on to implement two-level Iterative Refinement algorithms that will prove to be highly efficient.