OPICO 7: Verification

Part 7 in a series on: Optimization Problems with Items and Categories in Oracle

The knapsack problem is a problem in combinatorial optimization: Given a set of items, each with a weight and a value, determine the number of each item to include in a collection so that the total weight is less than or equal to a given limit and the total value is as large as possible.

• Knapsack problem

The knapsack problem and many other problems in combinatorial optimization require the selection of a subset of items to maximize an objective function subject to constraints. A common approach to solving these problems algorithmically involves recursively generating sequences of items of increasing length in a search for the best subset that meets the constraints.

I applied this kind of approach using SQL for a number of problems, starting in January 2013 with A Simple SQL Solution for the Knapsack Problem (SKP-1), and I wrote a summary article, Knapsacks and Networks in SQL, in December 2017 when I put the code onto GitHub, sql_demos - Brendan’s repo for interesting SQL.

This is the seventh in a series of eight articles that aim to provide a more formal treatment of algorithms for item sequence generation and optimization, together with practical implementations, examples and verification techniques in SQL and PL/SQL.

List of Articles

• OPICO 1: Algorithms for Item Sequence Generation
• OPICO 2: SQL for Item Sequence Generation
• OPICO 3: Algorithms for Item/Category Optimization
• OPICO 4: Recursive SQL for Item/Category Optimization
• OPICO 5: Tuning Recursive SQL for Item/Category Optimization
• OPICO 6: Mixed SQL and PL/SQL Methods for Item/Category Optimization
• OPICO 7: Verification
• OPICO 8: Automation

GitHub

• Optimization Problems with Items and Categories in Oracle
  [See README for references]

Twitter

• Thread with Short Recordings

In the sixth article, we explained how to use mixed SQL and PL/SQL methods to implement the algorithms described generically in the third.

In the current article, we discuss how to verify correctness of solution methods for algorithmic problems of this kind, using a number of approaches, including unit testing.

[Image from Pixabay]

Contents

↓ 1 The Verification Problem
↓ 2 Non-Unit Testing Approaches
↓ 3 Perturbation Analysis
↓ 4 Unit Testing
↓ 5 Conclusion

1 The Verification Problem

↑ Contents
↓ ChatGPT on NP Problems
↓ ChatGPT on Constraint vs Optimality Checking
↓ Conclusion

It’s important to verify that computer programs produce the correct results.

In many cases the programs we write can be considered as the automation of processing that could be performed manually. Verifying that a given output is correct is usually straightforward in these cases, although verifying that all outputs will be correct is more difficult, and is why automation of the verification process itself has become popular.

However, for programs with algorithms for solving optimization problems verification can be more difficult. In fact, there are a number of factors to consider, and in this section we include some interactions on the subject with the Artifical Intelligence tool ChatGPT. We found the interactions helpful in thinking about this area, although they also illustrate the well-known issue with current AI models that responses are often incorrect or only partially correct.

ChatGPT on NP Problems

↑ 1 The Verification Problem

[Image by Flybynight from Pixabay]

Those are my principles, and if you don't like them...well I have others.

― Groucho Marx (attributed)

ChatGPT Version

You are interacting with ChatGPT based on the GPT-4 architecture, specifically an implementation known as GPT-4-turbo. This version was developed by OpenAI and released in 2023

I asked ChatGPT the following question

there are certain types of problem where finding the solution is very hard but verifying correctness is easy, can you give some examples of this

ChatGPT Response:

Yes, there are several types of problems where finding the solution is very hard, but verifying the correctness of a given solution is relatively easy. These problems fall into a category known as **NP (nondeterministic polynomial time) problems** in computational complexity theory. Here are a few classic examples:

1. The Traveling Salesman Problem (TSP):
   • Problem: Given a list of cities and the distances between each pair of cities, find the shortest possible route that visits each city exactly once and returns to the origin city.
   • Verification: If someone provides a specific route, you can easily calculate the total distance and check if it is shorter than the previously known routes and if it visits each city exactly once.
2. Integer Factorization:
   • Problem: Given a large integer, find its prime factors.
   • Verification: If someone provides a set of prime factors, you can multiply them together to check if they produce the original integer.
3. Graph Coloring:
   • Problem: Given a graph, assign colors to each vertex so that no two adjacent vertices share the same color using at most ( k ) colors.
   • Verification: If someone provides a coloring, you can easily check that no two adjacent vertices have the same color.
4. Knapsack Problem:
   • Problem: Given a set of items, each with a weight and a value, determine the number of each item to include in a collection so that the total weight is less than or equal to a given limit and the total value is as large as possible.
   • Verification: If someone provides a selection of items, you can easily calculate the total weight and value to verify if it meets the constraints and maximizes the value.
5. Hamiltonian Path Problem:
   • Problem: Given a graph, find a path that visits each vertex exactly once.
   • Verification: If someone provides a path, you can easily check if it visits each vertex exactly once.
6. Sudoku:
   • Problem: Fill a 9x9 grid with digits so that each column, each row, and each of the nine 3x3 subgrids contain all of the digits from 1 to 9.
   • Verification: If someone provides a filled grid, you can easily check each row, column, and subgrid to ensure all digits from 1 to 9 are present without repetition.
7. Subset Sum Problem:
   • Problem: Given a set of integers, determine if there is a non-empty subset whose sum is equal to a given number.
   • Verification: If someone provides a subset, you can easily sum its elements to check if it equals the given number.

These problems illustrate the fundamental concept of NP problems, where solutions can be verified in polynomial time, but finding the solutions may require non-polynomial time, depending on the problem and the size of the input.

ChatGPT on Constraint vs Optimality Checking

↑ 1 The Verification Problem

The answer above from ChatGPT did not appear to be entirely correct, so I asked a follow-up question.

My follow-up question

for the knapsack problem you mention, verification that a solution maximises the value does not appear obviously to be easy

ChatGPT Response:

You're right. Verifying that a solution to the knapsack problem maximizes the value is not straightforward, as it involves checking against all possible combinations, which is computationally intensive. The key aspect that makes verifying solutions to NP problems easy is that we verify whether a given solution satisfies the constraints, not whether it is the optimal solution. For the knapsack problem, here’s a clearer distinction:

• Decision Version of Knapsack (an NP problem): Given a set of items, each with a weight and a value, and a weight limit (W), is there a subset of items whose total weight is ( <= W ) and whose total value is at least ( V )?
  • Verification: Given a subset of items, you can easily sum their weights to check if they are ( <= W ) and sum their values to check if they are ( >= V ). This verification is straightforward and can be done in polynomial time.
• Optimization Version of Knapsack (NP-hard problem): Given a set of items, each with a weight and a value, and a weight limit (W), find the subset of items that maximizes the total value while keeping the total weight ( <= W ).
  • Verification: Given a subset of items, you can verify whether it meets the weight constraint and calculate its total value. However, verifying that this subset is the optimal one (i.e., that no other subset with a higher total value exists) is not easy. This requires comparing it against all other possible subsets, which is computationally infeasible for large inputs.

Other Examples with Clearer Verification

To further illustrate the distinction, let's look at other problems where verifying a solution is indeed easy:

1. 3-SAT (Boolean Satisfiability Problem):
   • Problem: Given a Boolean formula in conjunctive normal form (CNF), determine if there is an assignment of truth values to variables that makes the formula true.
   • Verification: If someone provides a truth assignment, you can easily substitute the values into the formula and check if the formula evaluates to true.
2. Hamiltonian Path (Decision Version):
   • Problem: Given a graph, is there a path that visits each vertex exactly once?
   • Verification: If someone provides a path, you can check that it visits each vertex exactly once and that consecutive vertices in the path are connected by edges.

Summary

In NP problems, verifying a given solution is about checking if it satisfies the problem’s constraints, not necessarily if it is the best or optimal solution. The optimization versions of these problems are often harder because they require ensuring no better solution exists, which is computationally difficult.

Conclusion

↑ 1 The Verification Problem

As ChatGPT confirmed above, after an extra prompt, checking that a proposed solution to a problem of the knapsack variety satisfies the constraints is easy, but it is much harder to check optimality computationally for larger datasets.

In our case, we showed a query in OPICO 5: Tuning Recursive SQL for Item/Category Optimization that, for the solution records in the paths_ranked_v view, lists the item categories with minimum and maximum limits and the actual numbers, as well as the total price, allowing us to verify correctness easily. For example, for the best solution for the England dataset, with maximum price 900, it gives:

Total Value Total Price  Rank Position Min Actual  Max Player List
----------- ----------- ----- -------- --- ------- --- -------------------------
       1965         889     1 DF       3    <-3    5   165, 332, 569
                              FW       1      2    3   286, 533
                              GK       1    <-1->  1   549
                              MF       2      5->  5   661, 030, 265, 641, 177

We can easily see that all the constraints have been met.

This leaves the difficult problem of verifying optimality, and this can’t be done directly for a dataset as large as the England dataset. However, there are a number of approaches that can increase our confidence in the results obtained. We’ll look first at approaches other than unit testing, then will describe unit testing applied to a range of scenarios involving small datasets.

2 Non-Unit Testing Approaches

↑ Contents
↓ Problem Abstraction
↓ Mathematics
↓ Multiple Datasets
↓ Multiple Solution Methods
↓ Perturbation Analysis

Problem Abstraction

↑ 2 Non-Unit Testing Approaches

The concept of abstraction is at the heart of computer programming in many different ways, and using it appropriately here helps greatly in our verification problem.

I first addressed the optimization problems considered in these articles after reading a post on a technical forum, Processing Cost - How to catch a soccer team with the highest combined score?, where the problem was described in this way:

I want to get a soccer team with the highest combined score averages and participations considering all possible formations and my budget, but I'm not finding a way to get a cost effective processing.

I realised that this was best considered as an instance of a more general problem concerning items and categories, not just footballers and positions. Furthermore, we can express the problem in mathematical notation, using it to reason about solution algorithms, and we can then develop multiple solution methods, apply them to multiple datasets, and apply unit testing and other verification concepts to the solution methods.

Mathematics

↑ 2 Non-Unit Testing Approaches

In the first article, OPICO 1: Algorithms for Item Sequence Generation, we showed how item sequences of four different types can be generated recursively. Using mathematical symbolism, we showed conceptually how to generate all sequences of length k given all sequences of length k-1, and that we can start from a zero-length root sequence. This mathematical approach allows for precise statements of the ways that the methods work, and allows us to verify easily that they do in fact generate all the desired sequences.

In the third article, OPICO 3: Algorithms for Item/Category Optimization, we extended the mathematical approach, first to handle constraints on item measures and on item categories, and then to the problem of optimizing a value function subject to the constraints on the sequences. This allowed us to determine a set of simple conditions on the items considered at a given iteration, and on the allowable transitions from the previous to the next item. Again the mathematical approach allows us to verify correctness of the algorithms, as well as facilitating the use of logic to improve efficiency by truncating subsequences as early as possible.

In summary, we have followed a mathematical treatment of the algorithms considered in order to establish confidence in their validity. However, this does not mean that the computer programs implementing the algorithms are necessarily correct. There is in fact a mathematically based approach to verification of program correctness that has been a research subject for many years - Formal methods. As the Wikipedia article puts it:

In computer science, formal methods are mathematically rigorous techniques for the specification, development, analysis, and verification of software and hardware systems.

Unfortunately the methods remain extremely difficult to apply in practice, and we deal with this aspect of verification using more practical approaches, first by testing with multiple datasets, second by comparing multiple implementation methods, third by using perturbation analysis within datasets, and finally by unit testing, following the author’s own approach: The Math Function Unit Testing Design Pattern.

Multiple Datasets

↑ 2 Non-Unit Testing Approaches

As we have noted above, it’s too difficult to verify with datasets of realistic size directly. However, we apply unit testing using scenarios based on very small datasets, and in addition we developed a small demonstration dataset in the third article, where the problem is to find the best set of 3-item subsets from 6 items, which is small enough to verify manually.

We have two larger datasets where we can’t verify correctness manually, but we can compare results across different solution methods, and perform perturbation analyses within the datasets.

Multiple Solution Methods

↑ 2 Non-Unit Testing Approaches

Multiple solution methods were developed based on the concepts described in the third article. The methods fall into three main classes:

One-Level Iteration

• Recursive SQL methods: These use Oracle’s recursive subquery factoring feature to generate the sequences, with implementation variants
• PL/SQL base methods: These generate the sequences using PL/SQL to control an outer loop, with SQL inserting into temporary tables or arrays at each step, and with both recursive and iterative variants

Two-Level Iteration

• Iterative refinement methods: These use one-level iteration methods as a base scheme within an outer loop that sets the two value filtering parameters

In the fifth article we introduced two Value Filtering parameters, KEEP_NUM and MIN_VALUE, which are used to improve performance, based on concepts explained in the third article. The first one, KEEP_NUM, when set to a value greater than zero, introduces the possibility of sub-optimal solutions, but can be safely used to generate values for the second parameter, MIN_VALUE, on a subsequent run. We can gain confidence in the correctness of the underlying solution method implementations by comparing results with KEEP_NUM = 0, across the range of solution methods.

In total there were 15 distinct implementations, and results were consistent across all datasets.

Perturbation Analysis

↑ 2 Non-Unit Testing Approaches

In our constrained optimization problem we have limits on numbers of items in given categories, and also a maximum price limit. So far, these have just been constant values that are part of the dataset definition, but if we consider them as variables they can help to verify correctness of the solution methods. For example, if we ‘perturb’ the problem by relaxing a limit, say by increasing the maximum price, then logically the optimal values can only improve or stay the same: If we find a case where a solution value decreases then we know that the optimal solution has not been found.

In the next section we’ll apply this approach across all three example datasets using a range of price maxima.

3 Perturbation Analysis

↑ Contents
↓ Scripts
↓ Results
↓ Conclusion

Scripts

↑ 3 Perturbation Analysis
↓ SQL Script - item_cat_seqs_perturb.sql
↓ Powershell Script - run_perturb.ps1

SQL Script - item_cat_seqs_perturb.sql

↑ Scripts

This script takes the dataset code and the maximum price as parameters and runs the Iteratively_Refine_Iterate procedure to find the best TOP_N solutions, where the bind variable is set to 3 for the small dataset and 10 for the other two.

DEFINE DS = &1
DEFINE MAX_PRICE = &2
BREAK ON tot_value ON tot_price ON rnk ON category_id
@..\..\install_prereq\initspool item_cat_seqs_perturb_&DS._&MAX_PRICE
PROMPT Truncate paths
TRUNCATE TABLE paths
/
BEGIN
    :MAX_PRICE := &MAX_PRICE;
END;
/
@..\set_contexts
VAR TIMER_SET NUMBER
BEGIN
  :TIMER_SET := Timer_Set.Construct('Item_Cat_Seqs_Perturb');
END;
/
SET TIMING ON
VAR start_time VARCHAR2(30)
PROMPT Pop_Table_Iterate
BEGIN
  SELECT To_Char(SYSDATE, 'DD/MM/YYYY hh24:mi:ss')
    INTO :start_time
    FROM DUAL;
  Item_Cat_Seqs.Iteratively_Refine_Iterate(p_keep_start      => :KEEP_START,
                                           p_keep_factor     => :KEEP_FACTOR);
END;
/
SET LINES 220
COLUMN "Summary" FORMAT A200
PROMPT Iteratively_Refine_Iterate - 10'th to 1'st highest values, then corresponding prices
SELECT :MAX_PRICE || ', ' ||
       Max(CASE WHEN rnk = 10 THEN tot_value END) || ', ' ||
       Max(CASE WHEN rnk = 9 THEN tot_value END)  || ', ' ||
       Max(CASE WHEN rnk = 8 THEN tot_value END)  || ', ' ||
       Max(CASE WHEN rnk = 7 THEN tot_value END)  || ', ' ||
       Max(CASE WHEN rnk = 6 THEN tot_value END)  || ', ' ||
       Max(CASE WHEN rnk = 5 THEN tot_value END)  || ', ' ||
       Max(CASE WHEN rnk = 4 THEN tot_value END)  || ', ' ||
       Max(CASE WHEN rnk = 3 THEN tot_value END)  || ', ' ||
       Max(CASE WHEN rnk = 2 THEN tot_value END)  || ', ' ||
       Max(CASE WHEN rnk = 1 THEN tot_value END)  || '; Prices: ' ||
       Max(CASE WHEN rnk = 10 THEN tot_price END) || ', ' ||
       Max(CASE WHEN rnk = 9 THEN tot_price END)  || ', ' ||
       Max(CASE WHEN rnk = 8 THEN tot_price END)  || ', ' ||
       Max(CASE WHEN rnk = 7 THEN tot_price END)  || ', ' ||
       Max(CASE WHEN rnk = 6 THEN tot_price END)  || ', ' ||
       Max(CASE WHEN rnk = 5 THEN tot_price END)  || ', ' ||
       Max(CASE WHEN rnk = 4 THEN tot_price END)  || ', ' ||
       Max(CASE WHEN rnk = 3 THEN tot_price END)  || ', ' ||
       Max(CASE WHEN rnk = 2 THEN tot_price END)  || ', ' ||
       Max(CASE WHEN rnk = 1 THEN tot_price END)  || '; ' ||
       86400 * (SYSDATE -  To_Date(:start_time, 'DD/MM/YYYY hh24:mi:ss'))  || ' : Values, Prices, Seconds ' "Summary"
  FROM paths_ranked_v
 WHERE rnk <= :TOP_N
/
PROMPT Iteratively_Refine_Iterate - Best and Worst
WITH nos AS (
    SELECT Max(tot_value) KEEP (DENSE_RANK FIRST ORDER BY rnk) max_tot_value,
           Max(tot_price) KEEP (DENSE_RANK FIRST ORDER BY rnk) max_tot_price,
           Min(tot_value) KEEP (DENSE_RANK LAST ORDER BY rnk) min_tot_value,
           Min(tot_price) KEEP (DENSE_RANK LAST ORDER BY rnk) min_tot_price,
           86400 * (SYSDATE -  To_Date(:start_time, 'DD/MM/YYYY hh24:mi:ss')) secs
      FROM paths_ranked_v
     WHERE rnk <= :TOP_N
)
SELECT :MAX_PRICE || ', ' || Nvl(max_tot_value, 0) || ', ' || Nvl(min_tot_value, 0) || ', ' || secs ||
       ' - BEST (V, P): (' || max_tot_value || ', ' ||
       max_tot_price || '); WORST (V, P): (' ||
       min_tot_value || ', ' ||
       min_tot_price || '); Seconds: ' ||
       secs "Summary"
  FROM nos
/
PROMPT Iteratively_Refine_Iterate
SELECT path,
       tot_value,
       tot_price,
       rnk
  FROM paths_ranked_v
 WHERE rnk <= :TOP_N
ORDER BY rnk, tot_price
/
EXEC Timer_Set.Increment_Time(:TIMER_SET, 'Iteratively_Refine_Iterate - path level');
SET TIMING OFF
EXEC Utils.W(Timer_Set.Format_Results(:TIMER_SET));
@..\..\install_prereq\endspool

The SQL script writes to log file, Run-Perturb_nn.log, all the usual detailed instrumentation and results, and also writes a single line summary of the best values and prices that the Powershell script retrieves for its own, summary level, log file.

Powershell Script - run_perturb.ps1

↑ Scripts

This is the Powershell driver script that calls the SQL script for a range of values for the maximum price and produces a summary log file containing a line for each dataset and maximum price with the best values.

Date -format "dd-MMM-yy HH:mm:ss"
$startTime = Get-Date

$directories = Get-ChildItem -Directory | Where-Object { $_.Name -match "^perturb_\d+$" }
[int]$maxIndex = 0
if ($directories.Count -gt 0) {
    [int[]]$indexLis = $directories |
        ForEach-Object {
            $_.Name -replace 'perturb_', ''
        }
    $maxIndex = ($indexLis | Measure-Object -Maximum).Maximum
}
$nxtIndex = ($maxIndex + 1).ToString("D2")
$newDir = ('perturb_' + $nxtIndex)
New-Item ('perturb_' + $nxtIndex) -ItemType Directory

$logFile = $PSScriptRoot + '\Run-Perturb_' + $nxtIndex + '.log'
$ddl = 'c_temp_tables'
$inputs = [ordered]@{
    sml = [ordered]@{views_sml              = @()
                     item_cat_seqs_perturb  = @(3, 4, 5, 6, 7)}
    bra = [ordered]@{views_bra              = @()
                     item_cat_seqs_perturb  = @(8000, 10000, 12000, 14000, 16000, 18000, 20000, 22000, 24000)}
    eng = [ordered]@{views_eng              = @()
                     item_cat_seqs_perturb  = @(500, 600, 650, 700, 750, 800, 850, 900, 950, 1000, 1100)}
}

foreach($i in $inputs.Keys){
    Set-Location $newDir
    $i
    [string]$cmdLis = ('@..\' + $ddl + [Environment]::NewLine)
    $logLis = @()
    foreach($v in $inputs[$i]) {
        foreach($k in $v.Keys) {
            if($v[$k].length -eq 0) {
                $cmdLis += ('@..\' + $k + [Environment]::NewLine)
            }
            foreach($p in $v[$k]) {
                $newCmd = ('@..\' + $k + ' ' + $i + ' ' + $p[0])
                ("newCmd = " + $newCmd)
                $p
                $cmdLis += ($newCmd + [Environment]::NewLine)
                $logLis += ($k + '_' + $i + '_' + $p[0] + '.log')
            }
        }
    }
    $cmdLis
    $output = $cmdLis | sqlplus 'app/app@orclpdb'
    Set-Location ..

    foreach($l in $logLis) {
        $f = $newDir + '\' + $l
        $l | Out-File $logFile -Append -encoding utf8
        Get-Content $f | Select-String -Pattern '; Prices' | Out-File $logFile -Append -encoding utf8
    }
}
$elapsedTime = (Get-Date) - $startTime
$roundedTime = [math]::Round($elapsedTime.TotalSeconds)

"Total time taken: $roundedTime seconds" | Out-File $logFile -Append -encoding utf8

We can easily extract from the log file lines in CSV format with the maximum price followed by the best values in increasing order. These can then be used to obtain graphs of the results in Excel.

Results

↑ 3 Perturbation Analysis
↓ Small Dataset
↓ Brazil Dataset
↓ England Dataset

Small Dataset

↑ Results

For this dataset the top three solutions are requested. A maximum price of 3 returned no solutions, a maximum price of 4 returned only two solutions, and a maximum price of 7 returned the same solution set as a maximum price of 6.

For the small dataset we can include the actual prices and the solutions in our table, where V = value, P = price, Sol = solution.

Max Price	V / P / Sol 3	V / P / Sol 2	V / P / Sol 1
4	0 / 0 / NA	9 / 4 / 214	11 / 4 / 145
5	10 / 5 / 314	11 / 4 / 145	12 / 5 / 245
6	11 / 4 / 145	12 / 5 / 245	13 / 5 / 345
7	11 / 4 / 145	12 / 5 / 245	13 / 5 / 345

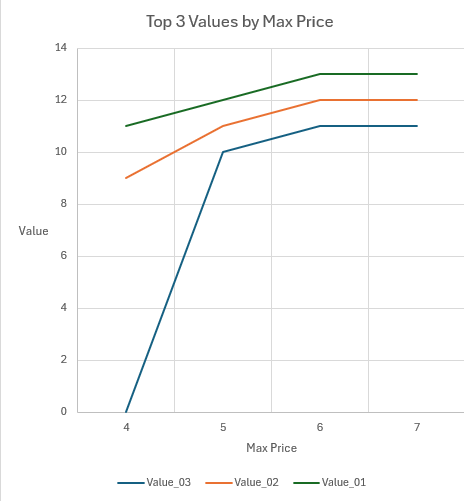
The graph shows that the values in each rank position increase monotically with maximum price, until maximum values are attained.

Brazil Dataset

↑ Results

For this dataset the top ten solutions are requested. A maximum price of 8000 returned no solutions, and a maximum price of 22000 returned the same solution set as a maximum price of 24000.

All solution sets were obtained in between 1 and 2 seconds.

Max Price	Value_10	Value_09	Value_08	Value_07	Value_06	Value_05	Value_04	Value_03	Value_02	Value_01	Seconds
10000	8548	8548	8556	8568	8569	8576	8586	8596	8609	8651	1
12000	9035	9041	9044	9068	9095	9118	9174	9191	9194	9201	2
14000	9724	9730	9731	9738	9745	9747	9754	9806	9813	9914	2
16000	10128	10130	10131	10135	10154	10193	10213	10215	10230	10233	1
18000	10642	10643	10663	10674	10692	10733	10740	10766	10772	10790	1
20000	10790	10807	10825	10825	10831	10833	10833	10905	10923	10923	1
22000	10833	10833	10845	10845	10865	10883	10883	10905	10923	10923	1
24000	10833	10833	10845	10845	10865	10883	10883	10905	10923	10923	1

The graph shows that the values in each rank position increase monotically with maximum price, until maximum values are attained.

England Dataset

↑ Results

For this dataset the top ten solutions are requested. A maximum price of 500 returned no solutions, and a maximum price of 1100 returned the same solution set as a maximum price of 1000.

All solution sets were obtained in between 3 and 7 seconds.

Max Price	Value_10	Value_09	Value_08	Value_07	Value_06	Value_05	Value_04	Value_03	Value_02	Value_01	Seconds
600	1314	1315	1318	1319	1322	1324	1327	1329	1329	1336	7
650	1494	1495	1496	1496	1497	1498	1500	1500	1502	1506	4
700	1587	1587	1588	1588	1589	1589	1591	1592	1593	1594	4
750	1718	1718	1718	1719	1719	1720	1722	1722	1723	1729	6
800	1819	1819	1819	1822	1823	1823	1824	1824	1826	1829	6
850	1906	1908	1910	1910	1912	1912	1914	1914	1915	1919	5
900	1965	1965	1965	1966	1966	1968	1968	1970	1971	1973	4
950	1990	1990	1992	1992	1994	1994	1995	1995	1997	1998	3
1000	1992	1992	1994	1994	1995	1995	1997	1997	1998	1998	4
1100	1992	1992	1994	1994	1995	1995	1997	1997	1998	1998	4

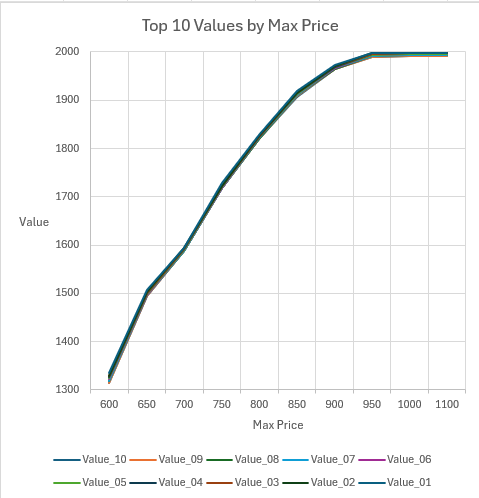
The graph shows that the values in each rank position increase monotically with maximum price, until maximum values are attained.

Conclusion

↑ 3 Perturbation Analysis

In all three datasets we see that each value in each rank position increases or stays the same as the maximum price increases, until at some threshold increasing the maximum price results in no further increases in value.

This is exactly as expected if the solution methods are working correctly.

We can also see that run times are all no more than a few seconds.

4 Unit Testing

↑ Contents
↓ Unit Testing for Optimization Problems
↓ Test Steps

The views are tested using The Math Function Unit Testing Design Pattern (general overview), described in its Oracle version here: Trapit - Oracle PL/SQL Unit Testing Module. In this approach, a ‘pure’ wrapper function is constructed that takes input parameters and returns a value, and is tested within a loop over scenario records read from a JSON file.

At a high level The Math Function Unit Testing Design Pattern involves three main steps:

1. Create an input file containing all test scenarios with input data and expected output data for each scenario
2. Create a results object based on the input file, but with actual outputs merged in
3. Use the results object to generate unit test results files formatted in HTML and/or text

Unit Testing for Optimization Problems

↑ 4 Unit Testing

We noted earlier that verification of programs for optimization problems tends to be more difficult than for more common types of processing.

In an article from October 2021, Unit Testing, Scenarios and Categories: The SCAN Method, I set out some ideas around choosing scenarios for unit testing in general. The basis of the SCAN method is that you consider the input space as viewed from the perspective of category sets, as many as are applicable to the unit under test. You then try to partition the space into categories within a category set where behaviour differs, or may differ, between categories: This allows for good test coverage to be obtained using a finite number of scenarios.

However, in the case of programs for solving optimization problems it seems more natural to consider some behaviours in terms of the output space than the input space. We saw in the section on perturbation analysis above that increasing the maximum price limit resulted in increases in the solution values up to a certain threshold, above which no further increases resulted; also, below another threshold no solutions were found. This corresponds to three categories of behaviour for the maximum price constraint. In the terminology of constrained optimization we would describe the constraint as being in one of three categories:

• Infeasible: Preventing any solution
• Binding (or Active): Restricting the optimal value, so that relaxing the constraint improves the optimal value
• Non-binding (or Inactive): Solutions are available but relaxing the constraint does not improve the optimal value

So, to apply our SCAN method to constrained optimization problems, we could consider the constraints (one each for lower and upper limits) to be category sets, using the above three categories in each case. [NB The use of the term category here has nothing to do with its use in item categories in our problem definitions]. In practice, for the small datasets appropriate for unit testing we can easily find inputs that result in the solutions matching the output space categories.

Alternatively, we could take as category sets Constraint Activity and Constraint Infeasibility, with the individual constraints being categories, as I have chosen to do in the sections below for convenience.

There will also be other category sets to consider, as described below.

Test Steps

↑ 4 Unit Testing
↓ Step 1: Create JSON File
↓ Step 2: Create Results Object
↓ Step 3: Format Results

Step 1: Create JSON File

↑ Test Steps
↓ Unit Test Wrapper Function
↓ Scenario Category ANalysis (SCAN)

Step 1 requires analysis to determine the extended signature for the unit under test, and to determine appropriate scenarios to test. The results of this analysis can be summarised in three CSV files which a powershell API, Write-UT_Template, uses as inputs to create a template for the JSON file.

This template file, tt_item_cat_seqs.purely_wrap_best_combis_temp.json, contains the full meta section (which describes groups and fields), and a set of template scenarios having name as scenario key, a category set attribute, and a single record with default values for each input and output group.

For each scenario element, we need to update the values to reflect the scenario to be tested, in the actual input JSON file, tt_item_cat_seqs.purely_wrap_best_combis_inp.json.

Unit Test Wrapper Function

↑ Step 1: Create JSON File

Here is a diagram of the input and output groups for this example:

From the input and output groups depicted we can construct CSV files with flattened group/field structures, and default values added, as follows (with tt_item_cat_seqs.purely_wrap_best_combis_inp.csv left, tt_item_cat_seqs.purely_wrap_best_combis_out.csv right):

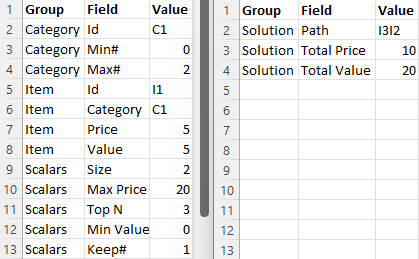
These form two of the three input files for the Powershell script that generates a template for the input JSON file. The third is the scenarios file, shown in the next section.

Scenario Category ANalysis (SCAN)

↑ Step 1: Create JSON File
↓ Generic Category Sets
↓ Categories and Scenarios

Generic Category Sets

↑ Scenario Category ANalysis (SCAN)

As explained in the article mentioned above, it can be very useful to think in terms of generic category sets that apply in many situations. In this case, where we are testing algorithms for a type of constrained optimization problem, constraint activity and constraint infeasibility would be generally useful.

Constraint Activity

In constrained optimization a constraint is said to be active if relaxing it would allow a higher value solution, and the categories would be the specific constraints present, as well as the case where none are active.

Code	Description
Unconstrained	No active constraint
Constraint x	Constraint x is active (repeated for each x)

Constraint Infeasibility

In constrained optimization a specific constraint may prevent any solution being possible, and the problem is said to be infeasible.

Code	Description
Feasible	Solutions exist
Constraint x	Constraint x renders problem infeasible (repeated for each x)

Multiplicity

The generic category set of multiplicity is applicable very frequently, and we should check each of the relevant categories.

Code	Description
None	No values
One	One value
Many	Many values

We apply it to the ItemCat entity, and with subtype of (Actual / Top N) to the Solution entity.

Categories and Scenarios

↑ Scenario Category ANalysis (SCAN)

After analysis of the possible scenarios in terms of categories and category sets, we can depict them on a Category Structure diagram:

We can tabulate the results of the category analysis, and assign a scenario against each category set/category with a unique description:

#	Category Set	Category	Scenario
1	Choose Range (r / n)	One / Multiple	Choose 1 / n
2	Choose Range (r / n)	Multiple / Multiple (r < n)	Choose r / n (r < n)
3	Choose Range (r / n)	Multiple / Multiple (r = n)	Choose n / n
4	ItemCat Multiplicity	None	No itemcats
5	ItemCat Multiplicity	One	One itemcat
6	ItemCat Multiplicity	Multiple	Multiple itemcats
7	ItemCat Range	Min Only	Itemcat min only
8	ItemCat Range	Max Only	Itemcat max only
9	ItemCat Range	Min < Max	Itemcat with min < max
10	ItemCat Range	Min = Max	Itemcat with min = max
11	Solution Multiplicity (Actual / Top N)	None / N	No solution (want top N)
12	Solution Multiplicity (Actual / Top N)	One / One	1 solution (want top 1)
13	Solution Multiplicity (Actual / Top N)	Multiple (=) / N	N solutions (want top N)
14	Solution Multiplicity (Actual / Top N)	Multiple (<) / N	< N solutions (want top N)
15	Constraint Activity	Unconstrained	No active constraint
16	Constraint Activity	Price Maximum	Price maximum active
17	Constraint Activity	ItemCat Minimum	Itemcat minimum active
18	Constraint Activity	ItemCat Maximum	Itemcat maximum active
19	Constraint Infeasibility	Feasible	Solutions exist
20	Constraint Infeasibility	Price Maximum	No solution - price maximum
21	Constraint Infeasibility	ItemCat Minimum	No solution - itemcat minimum
22	Constraint Infeasibility	ItemCat Maximum	No solution - itemcat maximum

From the scenarios identified we can construct the following CSV file (tt_item_cat_seqs.purely_wrap_best_combis_sce.csv), taking the category set and scenario columns, and adding an initial value for the active flag:

The powershell API to generate the template JSON file can be run with the following powershell in the folder of the CSV files:

Import-Module ..\powershell_utils\TrapitUtils\TrapitUtils
Write-UT_Template 'tt_item_cat_seqs.purely_wrap_best_combis' '|'

This creates the template JSON file, tt_item_cat_seqs.purely_wrap_best_combis_temp.json, in which, for each scenario element, we need to update the values to reflect the scenario to be tested, in the actual input JSON file, tt_item_cat_seqs.purely_wrap_best_combis_inp.json.

Step 2: Create Results Object

↑ Test Steps
↓ Call to Trapit_Run Packaged Function
↓ TT_Item_Cats Package

Step 2 requires the writing of a wrapper function that is called by a library packaged subprogram that runs all tests for a group name passed in as a parameter.

The library subprogram calls the wrapper function, specific to the unit under test, within a loop over the scenarios in the input JSON file. The names of the JSON file and of the wrapper function are assigned as part of the installation of the unit test data. The function specification is fixed for each function, as shown below, while the function body is specific to the unit under test.

The library subprogram writes the output JSON file with the actual results, obtained from the wrapper function, merged in along with the expected results.

In non-database languages, such as JavaScript or Python, the wrapper function can be defined in a script and passed as a parameter in a call to the library subprogram. In Oracle PL/SQL the wrapper function is defined in the database and called using dynamic PL/SQL from the library subprogram.

Call to Trapit_Run Packaged Function

↑ Step 2: Create Results Object

Unit tests are run by making a call to a library packaged function that runs all tests for a group name passed in as a parameter, ‘item_cat_seqs’ in this case.

FUNCTION Test_Output_Files(p_group_nm VARCHAR2) RETURN L1_chr_arr;

This function runs the tests for the input group leaving the output JSON files in the assigned directory on the database server, and returns the full file paths in an array.

The function is called by a Powershell script that combines steps 2 and 3, as shown in step 3 below.

TT_Item_Cats Package

↑ Step 2: Create Results Object
↓ Package Spec
↓ Package Body 1: Adding the test scenario data
↓ Package Body 2: Base function shared by public API functions
↓ Package Body 3: Public API functions

This package contains the wrapper functions called by the Trapit library package. Each solution method has its own wrapper function that calls a view from which the results are retrieved, and, optionally, a procedure to call to populate the view source.

The Math Function Unit Testing Design Pattern makes testing views very straightforward.

All 15 unit tests use the same input JSON file, with 22 scenarios.

A utility function, Utils.View_To_List, retrieves the results of querying the views into arrays of delimited strings that are then returned to the library package.

Package Spec

↑ TT_Item_Cats Package

Here is the package specification, with separate API functions for each view, all having the same parameter and return value type:

CREATE OR REPLACE PACKAGE TT_Item_Cat_Seqs AS
FUNCTION RSF_Post_Valid(
              p_inp_3lis                     L3_chr_arr)
              RETURN                         L2_chr_arr;
FUNCTION RSF_SQL(
              p_inp_3lis                     L3_chr_arr)
              RETURN                         L2_chr_arr;
FUNCTION RSF_SQL_Material(
              p_inp_3lis                     L3_chr_arr)
              RETURN                         L2_chr_arr;
FUNCTION RSF_Irk_IRS_Tabs(
              p_inp_3lis                     L3_chr_arr)
              RETURN                         L2_chr_arr;
FUNCTION RSF_Irk_Tab_Where_Fun(
              p_inp_3lis                     L3_chr_arr)
              RETURN                         L2_chr_arr;
FUNCTION Pop_Table_Iterate(
              p_inp_3lis                     L3_chr_arr)
              RETURN                         L2_chr_arr;
FUNCTION Pop_Table_Iterate_Base(
              p_inp_3lis                     L3_chr_arr)
              RETURN                         L2_chr_arr;
FUNCTION Pop_Table_Iterate_Link(
              p_inp_3lis                     L3_chr_arr)
              RETURN                         L2_chr_arr;
FUNCTION Pop_Table_Iterate_Base_Link(
              p_inp_3lis                     L3_chr_arr)
              RETURN                         L2_chr_arr;
FUNCTION Array_Iterate(
              p_inp_3lis                     L3_chr_arr)
              RETURN                         L2_chr_arr;
FUNCTION Pop_Table_Recurse(
              p_inp_3lis                     L3_chr_arr)
              RETURN                         L2_chr_arr;
FUNCTION Array_Recurse(
              p_inp_3lis                     L3_chr_arr)
              RETURN                         L2_chr_arr;
FUNCTION Iteratively_Refine_Recurse(
              p_inp_3lis                     L3_chr_arr)
              RETURN                         L2_chr_arr;
FUNCTION Iteratively_Refine_Iterate(
              p_inp_3lis                     L3_chr_arr)
              RETURN                         L2_chr_arr;
FUNCTION Iteratively_Refine_RSF(
              p_inp_3lis                     L3_chr_arr)
              RETURN                         L2_chr_arr;

END TT_Item_Cat_Seqs;

Package Body 1: Adding the test scenario data

↑ TT_Item_Cats Package

Here is the first section of the package body, with three functions to add the test scenario data:

CREATE OR REPLACE PACKAGE BODY TT_Item_Cat_Seqs AS

PROCEDURE add_Cats(
            p_cat_2lis                     L2_chr_arr) IS
BEGIN
  FOR i IN 1..p_cat_2lis.COUNT LOOP
    INSERT INTO small_categories VALUES (p_cat_2lis(i)(1), p_cat_2lis(i)(2), p_cat_2lis(i)(3));
  END LOOP;
END add_Cats;

PROCEDURE add_Items(
            p_item_2lis                    L2_chr_arr) IS
BEGIN
  FOR i IN 1..p_item_2lis.COUNT LOOP
    INSERT INTO small_items VALUES (p_item_2lis(i)(1), p_item_2lis(i)(1), p_item_2lis(i)(2), p_item_2lis(i)(3), p_item_2lis(i)(4));
  END LOOP;
END add_Items;

PROCEDURE add_Scalars(
            p_scalar_lis                   L1_chr_arr) IS
BEGIN
  Item_Cat_Seqs.Set_Contexts(
            p_seq_size       => p_scalar_lis(1),
            p_max_price      => p_scalar_lis(2),
            p_top_n          => p_scalar_lis(3),
            p_min_value      => p_scalar_lis(4),
            p_keep_num       => p_scalar_lis(5),
            p_item_width     => '2'); -- for post valid view
END add_Scalars;

Package Body 2: Base function shared by public API functions

↑ TT_Item_Cats Package

Here is the second section of the package body, with private function purely_Wrap_Best_Combis:

FUNCTION purely_Wrap_Best_Combis(
              p_view_name                    VARCHAR2,
              p_inp_3lis                     L3_chr_arr,
              p_proc_name                    VARCHAR2 := NULL)
              RETURN                         L2_chr_arr IS
  l_act_2lis        L2_chr_arr := L2_chr_arr();
  l_scalar_lis      L1_chr_arr := p_inp_3lis(3)(1);
  l_result_lis      L1_chr_arr;
  l_n_rows          PLS_INTEGER;
  l_path_len        PLS_INTEGER;
  l_params          VARCHAR2(4000);
BEGIN
  DELETE small_categories;
  DELETE small_items;
  add_Cats(p_cat_2lis       => p_inp_3lis(1));
  add_Items(p_item_2lis     => p_inp_3lis(2));
  add_Scalars(p_scalar_lis  => l_scalar_lis);
  IF p_proc_name IN ('Init_Loop', 'Iteratively_Refine_Iterate') THEN
    l_params := '(' || l_scalar_lis(5) || ', 10)';
  ELSIF p_proc_name = 'Init' OR p_proc_name LIKE 'Pop_Table%' THEN
    l_params := '(' || l_scalar_lis(5) || ', ' || l_scalar_lis(4) || ')';
  END IF;
  IF p_proc_name IS NOT NULL THEN
    EXECUTE IMMEDIATE 'BEGIN Item_Cat_Seqs.' || p_proc_name || l_params || '; END;';
  END IF;
  l_act_2lis.EXTEND;
  l_result_lis := Utils.View_To_List(
                                p_view_name     => p_view_name,
                                p_sel_value_lis => L1_chr_arr('path', 'tot_price', 'tot_value'),
                                p_where         => 'rnk <= ' || l_scalar_lis(3),
                                p_order_by      => 'rnk');
  l_path_len := 2 * To_Number(l_scalar_lis(1));
  l_act_2lis(1) := L1_chr_arr();
  FOR i IN 1..l_result_lis.COUNT LOOP
    l_act_2lis(1).EXTEND;
    l_act_2lis(1)(i) := Item_Cat_Seqs.Norm_Path(p_path      => Substr(l_result_lis(i), 1, l_path_len),
                                                p_token_len => 2) ||
                                                               Substr(l_result_lis(i), l_path_len + 1);
  END LOOP;
  ROLLBACK;
  RETURN l_act_2lis;
END purely_Wrap_Best_Combis;

• the function starts by deleting any existing data in the categories and items tables
• the scenario test data are then added using three private functions
• if a procedure call is needed to populate a results table it is executed, after creating a parameter string where necessary
• the results are obtained by a call to a utility function, Utils.View_To_List
• the library unit testing package allows for multiple groups of records, so that a two-level list is returned
• for testing views, only the first row is needed as there is only one group
• different solution methods may return solution paths with items in different orders, so we normalise the paths to ensure they all appear in the same order
• the data changes are rolled back before return

Package Body 3: Public API functions

↑ TT_Item_Cats Package

Here is the third section of the package body, with 15 public API functions, all of which simply call the shared base function, purely_Wrap_Best_Combis. They each pass in the name of the view from which the results are retrieved, the input data array, and, where necessary, a procedure to call to populate the view source.

FUNCTION RSF_Post_Valid(
              p_inp_3lis                     L3_chr_arr)
              RETURN                         L2_chr_arr IS
BEGIN
    RETURN purely_Wrap_Best_Combis(
              p_view_name   => 'rsf_post_valid_v',
              p_inp_3lis    => p_inp_3lis);
END RSF_Post_Valid;

FUNCTION RSF_SQL(
              p_inp_3lis                     L3_chr_arr)
              RETURN                         L2_chr_arr IS
BEGIN
    RETURN purely_Wrap_Best_Combis(
              p_view_name   => 'rsf_sql_v',
              p_inp_3lis    => p_inp_3lis);
END RSF_SQL;

FUNCTION RSF_SQL_Material(
              p_inp_3lis                     L3_chr_arr)
              RETURN                         L2_chr_arr IS
BEGIN
    RETURN purely_Wrap_Best_Combis(
              p_view_name   => 'rsf_sql_material_v',
              p_inp_3lis    => p_inp_3lis);
END RSF_SQL_Material;

FUNCTION RSF_Irk_IRS_Tabs(
              p_inp_3lis                     L3_chr_arr)
              RETURN                         L2_chr_arr IS
BEGIN
    RETURN purely_Wrap_Best_Combis(
              p_view_name   => 'rsf_irk_irs_tabs_v',
              p_inp_3lis    => p_inp_3lis,
              p_proc_name   => 'Init');
END RSF_Irk_IRS_Tabs;

FUNCTION RSF_Irk_Tab_Where_Fun(
              p_inp_3lis                     L3_chr_arr)
              RETURN                         L2_chr_arr IS
BEGIN
    RETURN purely_Wrap_Best_Combis(
              p_view_name   => 'rsf_irk_tab_where_fun_v',
              p_inp_3lis    => p_inp_3lis,
              p_proc_name   => 'Init');
END RSF_Irk_Tab_Where_Fun;

FUNCTION Pop_Table_Iterate(
              p_inp_3lis                     L3_chr_arr)
              RETURN                         L2_chr_arr IS
BEGIN

    RETURN purely_Wrap_Best_Combis(
              p_view_name   => 'paths_ranked_v',
              p_inp_3lis    => p_inp_3lis,
              p_proc_name   => 'Pop_Table_Iterate');

END Pop_Table_Iterate;

FUNCTION Pop_Table_Iterate_Base(
              p_inp_3lis                     L3_chr_arr)
              RETURN                         L2_chr_arr IS
BEGIN
    RETURN purely_Wrap_Best_Combis(
              p_view_name   => 'paths_base_ranked_v',
              p_inp_3lis    => p_inp_3lis,
              p_proc_name   => 'Pop_Table_Iterate_Base');
END Pop_Table_Iterate_Base;

FUNCTION Pop_Table_Iterate_Link(
              p_inp_3lis                     L3_chr_arr)
              RETURN                         L2_chr_arr IS
BEGIN
    RETURN purely_Wrap_Best_Combis(
              p_view_name   => 'paths_link_ranked_path_v',
              p_inp_3lis    => p_inp_3lis,
              p_proc_name   => 'Pop_Table_Iterate_Link');

END Pop_Table_Iterate_Link;
FUNCTION Pop_Table_Iterate_Base_Link(
              p_inp_3lis                     L3_chr_arr)
              RETURN                         L2_chr_arr IS
BEGIN
    RETURN purely_Wrap_Best_Combis(
              p_view_name   => 'paths_base_link_ranked_path_v',
              p_inp_3lis    => p_inp_3lis,
              p_proc_name   => 'Pop_Table_Iterate_Base_Link');
END Pop_Table_Iterate_Base_Link;

FUNCTION Array_Iterate(
              p_inp_3lis                     L3_chr_arr)
              RETURN                         L2_chr_arr IS
BEGIN
    RETURN purely_Wrap_Best_Combis(
              p_view_name   => 'array_iterate_v',
              p_inp_3lis    => p_inp_3lis,
              p_proc_name   => 'Init');
END Array_Iterate;

FUNCTION Pop_Table_Recurse(
              p_inp_3lis                     L3_chr_arr)
              RETURN                         L2_chr_arr IS
BEGIN
    RETURN purely_Wrap_Best_Combis(
              p_view_name   => 'paths_ranked_v',
              p_inp_3lis    => p_inp_3lis,
              p_proc_name   => 'Pop_Table_Recurse');
END Pop_Table_Recurse;

FUNCTION Array_Recurse(
              p_inp_3lis                     L3_chr_arr)
              RETURN                         L2_chr_arr IS
BEGIN
    RETURN purely_Wrap_Best_Combis(
              p_view_name   => 'array_recurse_v',
              p_inp_3lis    => p_inp_3lis,
              p_proc_name   => 'Init');
END Array_Recurse;

FUNCTION Iteratively_Refine_Recurse(
              p_inp_3lis                     L3_chr_arr)
              RETURN                         L2_chr_arr IS
BEGIN
    RETURN purely_Wrap_Best_Combis(
              p_view_name   => 'iteratively_refine_recurse_v',
              p_inp_3lis    => p_inp_3lis,
              p_proc_name   => 'Init_Loop');
END Iteratively_Refine_Recurse;

FUNCTION Iteratively_Refine_Iterate(
              p_inp_3lis                     L3_chr_arr)
              RETURN                         L2_chr_arr IS
BEGIN
    RETURN purely_Wrap_Best_Combis(
              p_view_name   => 'paths_ranked_v',
              p_inp_3lis    => p_inp_3lis,
              p_proc_name   => 'Iteratively_Refine_Iterate');
END Iteratively_Refine_Iterate;

FUNCTION Iteratively_Refine_RSF(
              p_inp_3lis                     L3_chr_arr)
              RETURN                         L2_chr_arr IS
BEGIN
    RETURN purely_Wrap_Best_Combis(
              p_view_name   => 'iteratively_refine_rsf_v',
              p_inp_3lis    => p_inp_3lis,
              p_proc_name   => 'Init_Loop');
END Iteratively_Refine_RSF;

END TT_Item_Cat_Seqs;

Step 3: Format Results

↑ Test Steps
↓ Running the Unit Tests
↓ Unit Test Report: Best Item Category Combis - Array_Iterate
↓ Scenario 2: Choose r / n (r < n) [Category Set: Choose Range (r / n)]
↓ Unit Test Report Locations

Step 3 involves formatting the results contained in the JSON output file from step 2, via the JavaScript formatter, and this step can be combined with step 2 for convenience.

Running the Unit Tests

↑ Step 3: Format Results

Test-FormatDB is the function from the TrapitUtils powershell package that calls the main test driver function, then passes the output JSON file name to the JavaScript formatter and outputs a summary of the results. It takes as parameters:

• unpw - Oracle user name / password string
• conn - Oracle connection string (such as the TNS alias)
• utGroup - Oracle unit test group
• testRoot - unit testing root folder, where results subfolders will be placed
• preSQL - SQL to execute first

Test-Format-Ico.ps1

Import-Module ..\powershell_utils\TrapitUtils\TrapitUtils
Test-FormatDB 'app/app' 'orclpdb' 'item_cat_seqs' $PSScriptRoot `
'BEGIN
    Utils.g_w_is_active := FALSE;
END;
/
@..\app\views_sml
'

This script calls the TrapitUtils library function Test-FormatDB, passing in for the preSQL parameter a SQL string to turn off logging to spool file, and to set the views to point to the sml dataset

The script creates a results subfolder for each unit in the ‘item_cat_seqs’ group, with results in text and HTML formats, in the script folder, and outputs the following summary:

File:          tt_item_cat_seqs.rsf_post_valid_out.json
Title:         Best Item Category Combis - RSF_Post_Valid
Inp Groups:    3
Out Groups:    2
Tests:         22
Fails:         0
Folder:        best-item-category-combis---rsf_post_valid

File:          tt_item_cat_seqs.rsf_sql_out.json
Title:         Best Item Category Combis - RSF_SQL
Inp Groups:    3
Out Groups:    2
Tests:         22
Fails:         0
Folder:        best-item-category-combis---rsf_sql

File:          tt_item_cat_seqs.rsf_sql_material_out.json
Title:         Best Item Category Combis - RSF_SQL_Material
Inp Groups:    3
Out Groups:    2
Tests:         22
Fails:         0
Folder:        best-item-category-combis---rsf_sql_material

File:          tt_item_cat_seqs.rsf_irk_irs_tabs_out.json
Title:         Best Item Category Combis - RSF_Irk_IRS_Tabs
Inp Groups:    3
Out Groups:    2
Tests:         22
Fails:         0
Folder:        best-item-category-combis---rsf_irk_irs_tabs

File:          tt_item_cat_seqs.rsf_irk_tab_where_fun_out.json
Title:         Best Item Category Combis - RSF_Irk_Tab_Where_Fun
Inp Groups:    3
Out Groups:    2
Tests:         22
Fails:         0
Folder:        best-item-category-combis---rsf_irk_tab_where_fun

File:          tt_item_cat_seqs.pop_table_iterate_out.json
Title:         Best Item Category Combis - Pop_Table_Iterate
Inp Groups:    3
Out Groups:    2
Tests:         22
Fails:         0
Folder:        best-item-category-combis---pop_table_iterate

File:          tt_item_cat_seqs.pop_table_iterate_base_out.json
Title:         Best Item Category Combis - Pop_Table_Iterate_Base
Inp Groups:    3
Out Groups:    2
Tests:         22
Fails:         0
Folder:        best-item-category-combis---pop_table_iterate_base

File:          tt_item_cat_seqs.pop_table_iterate_link_out.json
Title:         Best Item Category Combis - Pop_Table_Iterate_Link
Inp Groups:    3
Out Groups:    2
Tests:         22
Fails:         0
Folder:        best-item-category-combis---pop_table_iterate_link

File:          tt_item_cat_seqs.pop_table_iterate_base_link_out.json
Title:         Best Item Category Combis - Pop_Table_Iterate_Base_Link
Inp Groups:    3
Out Groups:    2
Tests:         22
Fails:         0
Folder:        best-item-category-combis---pop_table_iterate_base_link

File:          tt_item_cat_seqs.array_iterate_out.json
Title:         Best Item Category Combis - Array_Iterate
Inp Groups:    3
Out Groups:    2
Tests:         22
Fails:         0
Folder:        best-item-category-combis---array_iterate

File:          tt_item_cat_seqs.pop_table_recurse_out.json
Title:         Best Item Category Combis - Pop_Table_Recurse
Inp Groups:    3
Out Groups:    2
Tests:         22
Fails:         0
Folder:        best-item-category-combis---pop_table_recurse

File:          tt_item_cat_seqs.array_recurse_out.json
Title:         Best Item Category Combis - Array_Recurse
Inp Groups:    3
Out Groups:    2
Tests:         22
Fails:         0
Folder:        best-item-category-combis---array_recurse

File:          tt_item_cat_seqs.iteratively_refine_recurse_out.json
Title:         Best Item Category Combis - Iteratively_Refine_Recurse
Inp Groups:    3
Out Groups:    2
Tests:         22
Fails:         0
Folder:        best-item-category-combis---iteratively_refine_recurse

File:          tt_item_cat_seqs.iteratively_refine_iterate_out.json
Title:         Best Item Category Combis - Iteratively_Refine_Iterate
Inp Groups:    3
Out Groups:    2
Tests:         22
Fails:         0
Folder:        best-item-category-combis---iteratively_refine_iterate

File:          tt_item_cat_seqs.iteratively_refine_rsf_out.json
Title:         Best Item Category Combis - Iteratively_Refine_RSF
Inp Groups:    3
Out Groups:    2
Tests:         22
Fails:         0
Folder:        best-item-category-combis---iteratively_refine_rsf

Next we show the scenario-level summary of results for one of the 15 views tested.

Unit Test Report: Best Item Category Combis - Array_Iterate

↑ Step 3: Format Results

Here is the results summary in HTML format:

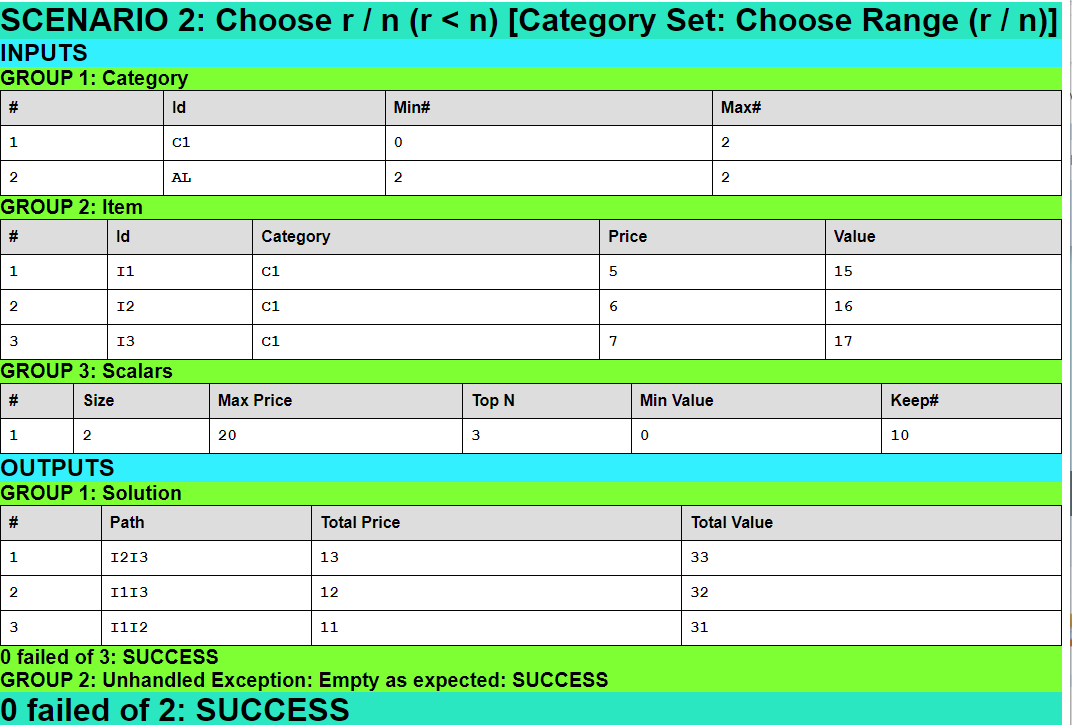
Scenario 2: Choose r / n (r < n) [Category Set: Choose Range (r / n)]

↑ Step 3: Format Results

Here is the result page for the second scenario, with empty output group 2, ‘Unhandled Exception’ being dynamically created by the library package to capture any unhandled exceptions, in HTML format:

Unit Test Report Locations

↑ Step 3: Format Results

You can review the formatted unit test results here, for one of the solution methods: Unit Test Report: Best Item Category Combis - Array_Iterate.

All results subfolders are available in the unit_test folder in the GitHub project, Optimization Problems with Items and Categories in Oracle, with, for example, the result files for the above solution method in the unit_test\best-item-category-combis---array_iterate subfolder [best-item-category-combis—array_iterate.html is the root page for the HTML version and best-item-category-combis—array_iterate.txt has the results in text format].

5 Conclusion

↑ Contents

In this article, we have discussed how to verify correctness of solution methods for algorithmic problems of this kind, using a number of approaches, including unit testing.

In the next article, we describe the various kinds of automation used in the development, testing and installation of the code and other artefacts for this series of articles.

• OPICO 1-8: Optimization Problems with Items and Categories in Oracle