OPICO 6: Mixed SQL and PL/SQL Methods for Item/Category Optimization
Part 6 in a series on: Optimization Problems with Items and Categories in Oracle
The knapsack problem is a problem in combinatorial optimization: Given a set of items, each with a weight and a value, determine the number of each item to include in a collection so that the total weight is less than or equal to a given limit and the total value is as large as possible.
The knapsack problem and many other problems in combinatorial optimization require the selection of a subset of items to maximize an objective function subject to constraints. A common approach to solving these problems algorithmically involves recursively generating sequences of items of increasing length in a search for the best subset that meets the constraints.
I applied this kind of approach using SQL for a number of problems, starting in January 2013 with A Simple SQL Solution for the Knapsack Problem (SKP-1), and I wrote a summary article, Knapsacks and Networks in SQL, in December 2017 when I put the code onto GitHub, sql_demos - Brendan’s repo for interesting SQL.
This is the sixth in a series of eight articles that aim to provide a more formal treatment of algorithms for item sequence generation and optimization, together with practical implementations, examples and verification techniques in SQL and PL/SQL.
List of Articles
- OPICO 1: Algorithms for Item Sequence Generation
- OPICO 2: SQL for Item Sequence Generation
- OPICO 3: Algorithms for Item/Category Optimization
- OPICO 4: Recursive SQL for Item/Category Optimization
- OPICO 5: Tuning Recursive SQL for Item/Category Optimization
- OPICO 6: Mixed SQL and PL/SQL Methods for Item/Category Optimization
- OPICO 7: Verification
- OPICO 8: Automation
GitHub 
- Optimization Problems with Items and Categories in Oracle
[See README for references]
Twitter 
In the fifth article we used two larger test datasets to analyse the performance of our initial recursive query, with Value Filtering techniques included, as described in the fourth article, and looked at variations on the query designed to improve performance.
In the current article, we demonstrate how PL/SQL can be used to implement both recursive and iterative versions of the basic one-level algorithm with embedded SQL, and we go on to implement a two-level Iterative Refinement algorithm that proves to be highly efficient.
The performance results cited are from instance 3 of running the driver script, Run-All.ps1: Run-All_03.log (summary) and results_03 folder (detail) in the GitHub project
[Image by Eugenio Hansen, OFS from Pixabay]
Contents
↓ 1 Recursion and Iteration: Process Flows
↓ 2 PL/SQL-Driven Solution Methods: Arrays and Temporary Tables
↓ 3 PL/SQL-Driven Solution Methods: Performance
↓ 4 Tuning Memory Usage
↓ 5 Iterative Refinement Algorithms
↓ 6 Conclusion
1 Recursion and Iteration: Process Flows
↑ Contents
↓ Recursion
↓ Iteration
This section has diagrams showing the process flows for recursive and iterative versions of the one-level algorithm using PL/SQL to control the flow, with embedded SQL inserting to temporary table or array. In a later section we will show PL/SQL implementations of the algorithm using the four combinations of recursion / iteration and table / array.
Recursion
↑ 1 Recursion and Iteration: Process Flows
The diagram below shows the process flow for a recursive algorithm for item/category sequence optimization.
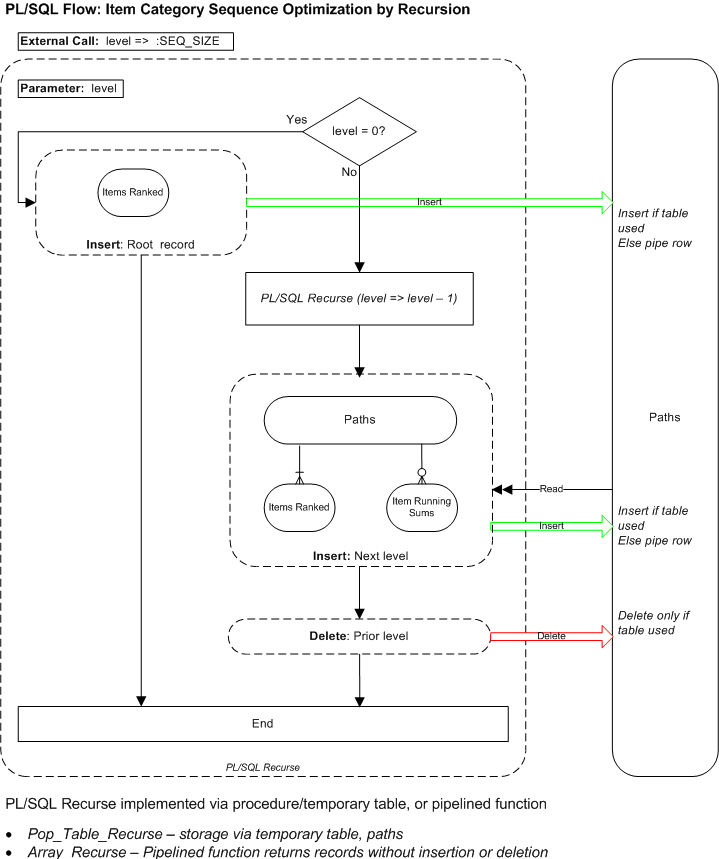
Iteration
↑ 1 Recursion and Iteration: Process Flows
The diagram below shows the process flow for an iterative algorithm for item/category sequence optimization.
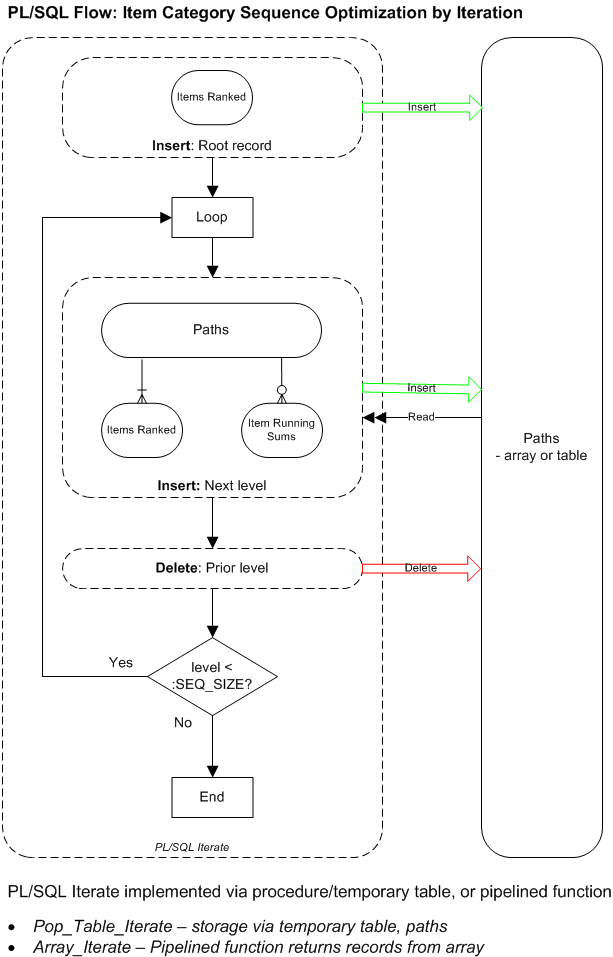
2 PL/SQL-Driven Solution Methods: Arrays and Temporary Tables
↑ Contents
↓ Common Procedures
↓ Paths Table Solution Methods
↓ Paths Array Solution Methods
In the sections below we show the PL/SQL and SQL code for four solution methods implementing recursive and iterative algorithms using both a temporary table and an array for the storage of intermediate paths.
- Table / Recursion - Pop_Table_Recurse
- Table / Iteration - Pop_Table_Iterate
- Array / Recursion - Array_Recurse
- Array / Iteration - Array_Iterate
In each case the steps from the set of subsequences of a given length to the set longer by one item is controlled within PL/SQL, either by iteration or recursion, instead of by recursive SQL. This results in simpler SQL, and in particular we no longer need to join the item running sums either as a table or an array, because at a given step its values are constants.
We’ll see later that different approaches show differences in performance characteristics, and that all are faster than recursive SQL.
Common Procedures
↑ 2 PL/SQL-Driven Solution Methods: Arrays and Temporary Tables
There is a driving procedure, Init, that is called at the start of each solution method. It first sets some package globals from system context values to simplify access throughout the package, and calls two procedures to populate each of the tables. These procedures are described in the earlier article, OPICO 5: Tuning Recursive SQL for Item/Category Optimization:
- Init: Driving procedure for the pre-calculations
- pop_Item_Running_Sums: Local procedure to populate the g_items_running_sum_lis array (IRS)
- pop_Items_Ranked: Local procedure to populate the ITEMS_RANKED index-organized table (IRK)
set_Sums
This procedure is called at the start of each iteration, and sets the globals, g_sum_price and g_sum_value, using the iteration number (or level) and the g_items_running_sum_lis array. These are referenced within the queries, avoiding the need for a table or array join.
PROCEDURE set_Sums(
p_iter PLS_INTEGER) IS
BEGIN
g_sum_price := 0;
g_sum_value := 0;
IF p_iter < g_seq_size then
g_sum_price := g_items_running_sum_lis(g_seq_size - p_iter).sum_price;
g_sum_value := g_items_running_sum_lis(g_seq_size - p_iter).sum_value;
END IF;
END set_Sums;
Paths Table Solution Methods
↑ 2 PL/SQL-Driven Solution Methods: Arrays and Temporary Tables
↓ Common View - PATHS_RANKED_V
↓ Common Procedures - Paths
↓ Table / Recursion - Pop_Table_Recurse
↓ Table / Iteration - Pop_Table_Iterate
The two solution methods based on a temporary table, PATHS, use a common view, PATHS_RANKED_V, that ranks the records in the table, after its population by their respective procedures.
Both table solution methods populate the PATHS table via a call to their own procedure, which calls the common initialization procedure at the start to pre-populate the g_items_running_sum_lis array and the ITEMS_RANKED index-organized table.
Common View - PATHS_RANKED_V
↑ Paths Table Solution Methods
This view reads the temporary table PATHS, and ranks the records.
CREATE OR REPLACE VIEW paths_ranked_v AS
SELECT path,
tot_price,
tot_value,
Row_Number() OVER (ORDER BY tot_value DESC, tot_price) rnk
FROM paths
Common Procedures - Paths
↑ Paths Table Solution Methods
↓ insert_Initial_Path
↓ insert_Paths
The two solution methods based on a temporary table, PATHS, use common procedures to insert the initial, root, PATHS record, and the subsequent records.
insert_Initial_Path
This procedure inserts the root record with a next_cat_id value taken from the item ranking first in ITEMS_RANKED.
PROCEDURE insert_Initial_Path(
p_timer_set PLS_INTEGER) IS
BEGIN
DELETE paths;
INSERT INTO paths (
path_rnk, item_rnk, lev, tot_price, tot_value, cat_id, next_cat_id, same_cats, min_items, cats_path, path
)
SELECT 0, 0, 0, 0, 0, 'AL', cat_id, 0, 0, '',''
FROM items_ranked
WHERE item_rnk = 1;
END insert_Initial_Path;
insert_Paths
This procedure inserts the records at each subsequent iteration.
Notice that there is no join to an item running sums collection as there was in the recursive SQL solution methods of the previous article, because the values are now constants (g_sum_price, g_sum_value) during a single iteration.
PROCEDURE insert_Paths(
p_timer_set PLS_INTEGER,
p_iter PLS_INTEGER) IS
BEGIN
set_Sums(p_iter => p_iter);
INSERT INTO paths (
path_rnk, item_rnk, lev, tot_price, tot_value, cat_id, next_cat_id, same_cats, min_items, cats_path, path
)
WITH path_join AS (
SELECT Row_Number() OVER (PARTITION BY trw.cats_path || irk.cat_id ORDER BY trw.tot_value + irk.item_value DESC, trw.tot_price + irk.item_price) path_rnk,
irk.item_rnk,
p_iter lev,
trw.tot_price + irk.item_price tot_price,
trw.tot_value + irk.item_value tot_value,
irk.cat_id,
irk.next_cat_id,
CASE irk.cat_id WHEN trw.cat_id THEN trw.same_cats + 1 ELSE 1 END same_cats,
irk.min_items,
trw.cats_path || irk.cat_id cats_path,
trw.path || irk.item_id path
FROM paths trw
JOIN items_ranked irk
ON irk.item_rnk BETWEEN (trw.item_rnk + 1) AND (irk.n_items - (g_seq_size - trw.lev - 1))
WHERE trw.tot_price + irk.item_price + g_sum_price <= g_max_price
AND trw.tot_value + irk.item_value + g_sum_value >= g_min_value
AND trw.lev < g_seq_size
AND CASE irk.cat_id WHEN trw.cat_id THEN trw.same_cats + 1 ELSE 1 END <= irk.max_items
AND g_seq_size - (trw.lev + 1) + Least(CASE irk.cat_id
WHEN trw.cat_id THEN trw.same_cats + 1 ELSE 1 END,
irk.min_items)
>= irk.min_remain
AND (irk.cat_id = trw.cat_id OR trw.same_cats >= trw.min_items)
AND (irk.cat_id = trw.cat_id OR irk.cat_id = Nvl(trw.next_cat_id, irk.cat_id))
)
SELECT path_rnk,
item_rnk,
lev,
tot_price,
tot_value,
cat_id,
next_cat_id,
same_cats,
min_items,
cats_path,
path
FROM path_join
WHERE path_rnk <= g_keep_num OR g_keep_num = 0;
DELETE paths WHERE lev = p_iter - 1;
END insert_Paths;
Table / Recursion - Pop_Table_Recurse
↑ Paths Table Solution Methods
Table / Recursion Driving Block
The table / recursion solution method uses a driving block to populate the PATHS table, via a call to the procedure Pop_Table_Recurse, which is then queried via the view PATHS_RANKED_V.
BEGIN
Item_Cat_Seqs.Pop_Table_Recurse(p_keep_num => &KEEP_NUM,
p_min_value => &MIN_VALUE);
END;
Procedure - Pop_Table_Recurse
This procedure implements the table / recursion solution, with the procedure calling itself recursively.
PROCEDURE Pop_Table_Recurse(
p_keep_num PLS_INTEGER,
p_min_value PLS_INTEGER,
p_timer_set PLS_INTEGER := NULL,
p_lev PLS_INTEGER := NULL) IS
l_timer_set PLS_INTEGER := p_timer_set;
BEGIN
IF p_timer_set IS NULL THEN
Init(p_keep_num => p_keep_num,
p_min_value => p_min_value);
END IF;
IF p_lev = 0 THEN
insert_Initial_Path(p_timer_set => l_timer_set);
RETURN;
END IF;
Pop_Table_Recurse(p_keep_num => p_keep_num,
p_min_value => p_min_value,
p_timer_set => l_timer_set,
p_lev => Nvl(p_lev, g_seq_size) - 1);
insert_Paths(p_timer_set => l_timer_set,
p_iter => Nvl(p_lev, g_seq_size));
END Pop_Table_Recurse;
Table / Iteration - Pop_Table_Iterate
↑ Paths Table Solution Methods
Table / Iteration Driving Block
The table / iteration solution method uses a driving block to populate the PATHS table, via a call to the procedure Pop_Table_Iterate, which is then queried via the view PATHS_RANKED_V.
BEGIN
Item_Cat_Seqs.Pop_Table_Iterate(p_keep_num => &KEEP_NUM,
p_min_value => &MIN_VALUE);
END;
Procedure - Pop_Table_Iterate
This procedure implements the table / iteration solution method, with the procedure having a loop over the sequence slots, with a call to the procedure insert_Paths inside the loop.
PROCEDURE Pop_Table_Iterate(
p_keep_num PLS_INTEGER,
p_min_value PLS_INTEGER) IS
BEGIN
Init(p_keep_num => p_keep_num,
p_min_value => p_min_value);
insert_Initial_Path(p_timer_set => l_timer_set);
FOR i IN 1..g_seq_size LOOP
insert_Paths(p_timer_set => l_timer_set,
p_iter => i);
END LOOP;
END Pop_Table_Iterate;
Paths Array Solution Methods
↑ 2 PL/SQL-Driven Solution Methods: Arrays and Temporary Tables
↓ Array Driving Block
↓ Common Function - Initial Path
↓ Array / Recursion - Array_Recurse
↓ Array / Iteration - Array_Iterate
The two array solution methods call the Init driving procedure first, to populate the item temporary tables, then call pipelined functions from their respective views, since functions called from a query can’t effect any DML.
Array Driving Block
↑ Paths Array Solution Methods
Both array solution methods uses a common driving block to pre-populate the the array g_items_running_sum_lis and the index-organized table ITEMS_RANKED, using the common procedure Init.
BEGIN
Item_Cat_Seqs.Init(p_keep_num => &KEEP_NUM,
p_min_value => &MIN_VALUE);
END;
Common Function - Initial Path
↑ Paths Array Solution Methods
Both array solution methods use a common function to return the initial root record. The function returns the root record with a next_cat_id value taken from the item ranking first in ITEMS_RANKED.
FUNCTION initial_Path
RETURN paths%ROWTYPE IS
l_paths_rec paths%ROWTYPE;
BEGIN
SELECT 0, 0, 0, 0, 0, 'AL', cat_id, 0, 0, '',''
INTO l_paths_rec
FROM items_ranked
WHERE item_rnk = 1;
RETURN l_paths_rec;
END initial_Path;
Array / Recursion - Array_Recurse
↑ Paths Array Solution Methods
View - ARRAY_RECURSE_V
This view calls the array / recursion function Array_Recurse, and ranks the records it returns.
CREATE OR REPLACE VIEW array_recurse_v AS
SELECT path,
tot_value,
tot_price,
Row_Number() OVER (ORDER BY tot_value DESC, tot_price) rnk
FROM TABLE(Item_Cat_Seqs.Array_Recurse)
Function - Array_Recurse
This function implements the array / recursion solution method, with the function having a recursive call to itself from the cursor within the loop that pipes out its result records in array form.
Notice that there is no join to an item running sums collection as there was in the recursive SQL solution methods of the previous article, because the values are now constants (g_sum_price, g_sum_value) during a single iteration.
FUNCTION Array_Recurse(
p_timer_set PLS_INTEGER := NULL,
p_lev PLS_INTEGER := NULL)
RETURN paths_arr PIPELINED IS
BEGIN
IF p_lev = 0 THEN
PIPE ROW(initial_Path);
RETURN;
END IF;
set_Sums(p_iter => p_lev);
FOR rec IN (
WITH path_join AS (
SELECT Row_Number() OVER (PARTITION BY trw.cats_path || irk.cat_id ORDER BY trw.tot_value + irk.item_value DESC, trw.tot_price + irk.item_price) path_rnk,
irk.item_rnk,
trw.lev + 1 lev,
trw.tot_price + irk.item_price tot_price,
trw.tot_value + irk.item_value tot_value,
irk.cat_id,
irk.next_cat_id,
CASE irk.cat_id WHEN trw.cat_id THEN trw.same_cats + 1 ELSE 1 END same_cats,
irk.min_items,
trw.cats_path || irk.cat_id cats_path,
trw.path || irk.item_id path
FROM Array_Recurse(p_timer_set => l_timer_set,
p_lev => Nvl(p_lev, g_seq_size) - 1) trw
JOIN items_ranked irk
ON irk.item_rnk BETWEEN (trw.item_rnk + 1) AND (irk.n_items - (g_seq_size - trw.lev - 1))
WHERE trw.tot_price + irk.item_price + g_sum_price <= g_max_price
AND trw.tot_value + irk.item_value + g_sum_value >= g_min_value
AND trw.lev < g_seq_size
AND CASE irk.cat_id WHEN trw.cat_id THEN trw.same_cats + 1 ELSE 1 END <= irk.max_items
AND g_seq_size - (trw.lev + 1) + Least(CASE irk.cat_id
WHEN trw.cat_id THEN trw.same_cats + 1 ELSE 1 END,
irk.min_items)
>= irk.min_remain
AND (irk.cat_id = trw.cat_id OR trw.same_cats >= trw.min_items)
AND (irk.cat_id = trw.cat_id OR irk.cat_id = Nvl(trw.next_cat_id, irk.cat_id))
)
SELECT path_rnk,
item_rnk,
lev,
tot_price,
tot_value,
cat_id,
next_cat_id,
same_cats,
min_items,
cats_path,
path
FROM path_join
WHERE path_rnk <= g_keep_num OR g_keep_num = 0) LOOP
PIPE ROW(rec);
END LOOP;
END Array_Recurse;
Array / Iteration - Array_Iterate
↑ Paths Array Solution Methods
View - ARRAY_ITERATE_V
This view calls the array / iteration function Array_Iterate, and ranks the records it returns.
CREATE OR REPLACE VIEW array_iterate_v AS
SELECT path,
tot_value,
tot_price,
Row_Number() OVER (ORDER BY tot_value DESC, tot_price) rnk
FROM TABLE(Item_Cat_Seqs.Array_Iterate)
Function - Array_Iterate
This function implements the array / iteration solution method, with the function having a loop over the sequence slots, with a recursive call to itself within the loop BULK COLLECT query. The paths array collected replaces the previous array at each iteration.
Notice that there is no join to an item running sums collection as there was in the recursive SQL solution methods of the previous article, because the values are now constants (g_sum_price, g_sum_value) during a single iteration.
FUNCTION Array_Iterate
RETURN paths_arr PIPELINED IS
l_paths_lis paths_arr := paths_arr(initial_Path);
l_paths_new_lis paths_arr;
BEGIN
FOR i IN 1..g_seq_size LOOP
set_Sums(p_iter => i);
WITH path_join AS (
SELECT Row_Number() OVER (PARTITION BY trw.cats_path || irk.cat_id ORDER BY trw.tot_value + irk.item_value DESC, trw.tot_price + irk.item_price) path_rnk,
irk.item_rnk,
trw.lev + 1 lev,
trw.tot_price + irk.item_price tot_price,
trw.tot_value + irk.item_value tot_value,
irk.cat_id,
irk.next_cat_id,
CASE irk.cat_id WHEN trw.cat_id THEN trw.same_cats + 1 ELSE 1 END same_cats,
irk.min_items,
trw.cats_path || irk.cat_id cats_path,
trw.path || irk.item_id path
FROM TABLE(l_paths_lis) trw
JOIN items_ranked irk
ON irk.item_rnk BETWEEN (trw.item_rnk + 1) AND (irk.n_items - (g_seq_size - trw.lev - 1))
WHERE trw.tot_price + irk.item_price + g_sum_price <= g_max_price
AND trw.tot_value + irk.item_value + g_sum_value >= g_min_value
AND trw.lev < g_seq_size
AND CASE irk.cat_id WHEN trw.cat_id THEN trw.same_cats + 1 ELSE 1 END <= irk.max_items
AND g_seq_size - (trw.lev + 1) + Least(CASE irk.cat_id
WHEN trw.cat_id THEN trw.same_cats + 1 ELSE 1 END,
irk.min_items)
>= irk.min_remain
AND (irk.cat_id = trw.cat_id OR trw.same_cats >= trw.min_items)
AND (irk.cat_id = trw.cat_id OR irk.cat_id = Nvl(trw.next_cat_id, irk.cat_id))
)
SELECT
path_rnk,
item_rnk,
lev,
tot_price,
tot_value,
cat_id,
next_cat_id,
same_cats,
min_items,
cats_path,
path
BULK COLLECT INTO l_paths_new_lis
FROM path_join
WHERE path_rnk <= g_keep_num OR g_keep_num = 0;
IF i < g_seq_size THEN
l_paths_lis := l_paths_new_lis;
END IF;
END LOOP;
FOR i IN 1..l_paths_new_lis.COUNT LOOP
PIPE ROW(l_paths_new_lis(i));
END LOOP;
END Array_Iterate;
3 PL/SQL-Driven Solution Methods: Performance
↑ Contents
↓ Results Summary
↓ Code Timing
↓ Execution Plans
Results of testing are summarised for the smaller, Brazil, and larger, England, datasets. Then a table of code timing results is given showing detailed row counts and timings by iteration for one of the solution methods. Finally, execution plans are shown for each method.
Results Summary
↑ 3 PL/SQL-Driven Solution Methods: Performance
↓ Solution Methods
↓ Brazil Dataset
↓ England Dataset
Solution Methods
This table shows the different solution methods tested, and assigns a short code to each one for convenience.
| Code | Procedure / Function | Table / Array | Recurse / Iterate |
|---|---|---|---|
| PTR | Pop_Table_Recurse | Table | Recurse |
| PTI | Pop_Table_Iterate | Table | Iterate |
| ARE | Array_Recurse | Array | Recurse |
| AIT | Array_Iterate | Array | Iterate |
Brazil Dataset
Solutions
Two solutions were found across the four pairs of parameters, one, B-B, suboptimal and the other, B-A, optimal:
Solution B-A (optimal)
Path Total Value Total Price Rank
------------------------------------ ----------- ----------- -----
078022098099058059060001002003038039 10923 18176 1
078023098099058059060001002003038039 10905 18795 2
078022098102058059060001002003038039 10833 18994 3
078022098099058059060001002003038040 10825 18190 4
078023098099058059060001002003038040 10807 18809 5
078022098099058059061001002003038039 10791 18915 6
078022098099058059060001002004038039 10790 17201 7
078021098099058059060001002004038039 10790 18052 8
078023098099058059060001002004038039 10772 17820 9
078022098099058059060001002003038041 10766 17948 10
Solution B-B (suboptimal)
Path Total Value Total Price Rank
------------------------------------ ----------- ----------- -----
078022098099058059060001002003038039 10923 18176 1
078023098099058059060001002003038039 10905 18795 2
078022098099058059060001002003038040 10825 18190 3
078023098099058059060001002003038040 10807 18809 4
078022098099058059060001002004038039 10790 17201 5
078021098099058059060001002004038039 10790 18052 6
078023098099058059060001002004038039 10772 17820 7
078022098099058059060001002003038041 10766 17948 8
078021098099058059060001002003038041 10766 18799 9
078022098099058059060061001002003038 10748 18209 10
Execution Times (Seconds)
| KEEP_NUM | MIN_VALUE | Solution Set | PTR | PTI | ARE | AIT |
|---|---|---|---|---|---|---|
| 10 | 0 | B-B (suboptimal) | 0.4 | 0.4 | 0.4 | 0.4 |
| 100 | 0 | B-A (optimal) | 0.6 | 0.6 | 0.6 | 0.6 |
| 100 | 10748 | B-A (optimal) | 0.4 | 0.4 | 0.4 | 0.4 |
| 0 | 10748 | B-A (optimal) | 0.4 | 0.4 | 0.4 | 0.4 |
None of the execution times exceed a second here, and there is little to distinguish the different solution methods on this smaller dataset.
England Dataset
Solutions
Two solutions were found across the four pairs of parameters, one, E-B, suboptimal and the other, E-A, optimal:
Solution E-A (optimal)
Path Total Value Total Price Rank
--------------------------------- ----------- ----------- -----
037024160463488298027452193344166 1965 889 1
037024160264488298045027452193166 1965 890 2
037024160463488298044027452193344 1963 890 3
037024160463488298044027452193166 1962 884 4
037024160264488298314027452193166 1962 885 5
037024160272488298044027452193166 1962 889 6
252024160264488298044027452193166 1959 889 7
037024160463488298045027452193344 1958 887 8
037024160463488298045027452193166 1957 881 9
037024160463488298314027452328166 1957 886 10
Solution E-B (suboptimal)
Path Total Value Total Price Rank
--------------------------------- ----------- ----------- -----
037024160463488298027452193344166 1965 889 1
037024160264488298045027452193166 1965 890 2
037024160463488298044027452193344 1963 890 3
037024160463488298044027452193166 1962 884 4
037024160264488298314027452193166 1962 885 5
037024160272488298044027452193166 1962 889 6
037024160264488298027452193344478 1957 887 7
037024160264488298027452193166478 1956 881 8
037024160264488298044027452193478 1954 882 9
037024160264488298027452193166460 1952 886 10
Execution Times (Seconds)
| KEEP_NUM | MIN_VALUE | Solution Set | PTR | PTI | ARE | AIT |
|---|---|---|---|---|---|---|
| 50 | 0 | E-B (suboptimal) | 1 | 1 | 2 | 2 |
| 300 | 0 | E-A (optimal) | 7 | 7 | 9 | 9 |
| 300 | 1952 | E-A (optimal) | 1 | 1 | 1 | 1 |
| 0 | 1952 | E-A (optimal) | 83 | 81 | 140 | 116 |
On this larger dataset we can see performance differences across the solution methods, particularly on the hardest parameter pair, (0, 1952).
The two Table methods perform similarly, at around 82 seconds. The Array / Recurse method is much worse at 140 seconds, and the Array / Iterate method took 116 seconds.
Using arrays in SQL can lead to performance problems owing to lack of good cardinality estimates, and the execution plan for Array / Recurse, shown in the next section, is perhaps suboptimal for that reason, with the execution time being 70% longer on the hardest parameter pair, (0, 1952). However, the plan for Array / Iterate was similar to that of the Table methods and was still significantly slower on (0, 1952), with the execution time being 40% longer.
Code Timing
↑ 3 PL/SQL-Driven Solution Methods: Performance
Each solution method was instrumented using the author’s own code timing package Oracle PL/SQL code timing module. Here are the results for the Pop_Table_Iterate solution on the England dataset with KEEP_NUM = 0 and MIN_VALUE = 1952. The INSERT and DELETE statements are timed separately at each iteration. The code timing package allows the timer name to include the rows processed, as shown below, providing quite detailed statistics at each iteration within PL/SQL.
Timer Set: Pop_Table_Iterate, Constructed at 10 Jun 2024 23:39:03, written at 23:40:24
======================================================================================
Timer Elapsed CPU Calls Ela/Call CPU/Call
------------------------ ---------- ---------- ---------- ------------- -------------
Initial delete (0) 0.01 0.01 1 0.00900 0.01000
Initial insert (1) 0.00 0.00 1 0.00000 0.00000
Insert paths 1 (17) 0.00 0.00 1 0.00000 0.00000
Delete paths 1 (1) 0.00 0.00 1 0.00000 0.00000
Insert paths 2 (290) 0.00 0.01 1 0.00400 0.01000
Delete paths 2 (17) 0.00 0.00 1 0.00000 0.00000
Insert paths 3 (553) 0.03 0.02 1 0.03100 0.02000
Delete paths 3 (290) 0.00 0.00 1 0.00000 0.00000
Insert paths 4 (279) 0.06 0.06 1 0.05600 0.06000
Delete paths 4 (553) 0.00 0.00 1 0.00000 0.00000
Insert paths 5 (1252) 0.03 0.03 1 0.03100 0.03000
Delete paths 5 (279) 0.00 0.00 1 0.00000 0.00000
Insert paths 6 (15349) 0.12 0.11 1 0.12000 0.11000
Delete paths 6 (1252) 0.00 0.01 1 0.00200 0.01000
Insert paths 7 (110100) 1.19 1.12 1 1.18700 1.12000
Delete paths 7 (15349) 0.02 0.01 1 0.01500 0.01000
Insert paths 8 (460638) 6.32 6.11 1 6.31600 6.11000
Delete paths 8 (110100) 0.11 0.07 1 0.10700 0.07000
Insert paths 9 (864748) 21.31 20.49 1 21.31400 20.49000
Delete paths 9 (460638) 0.41 0.30 1 0.41000 0.30000
Insert paths 10 (389615) 35.84 35.50 1 35.83500 35.50000
Delete paths 10 (864748) 0.68 0.42 1 0.67900 0.42000
Insert paths 11 (50) 14.29 14.24 1 14.29100 14.24000
Delete paths 11 (389615) 0.31 0.22 1 0.30500 0.22000
(Other) 0.00 0.00 1 0.00000 0.00000
------------------------ ---------- ---------- ---------- ------------- -------------
Total 80.71 78.73 25 3.22848 3.14920
------------------------ ---------- ---------- ---------- ------------- -------------
[Timer timed (per call in ms): Elapsed: 0.00952, CPU: 0.01143]
The Insert rows and times have been extracted to an Excel file, and the times were normalized so that the maximum normalized time equals the maximum number of rows. The rows and normalized times have then been plotted on a graph against the iteration.
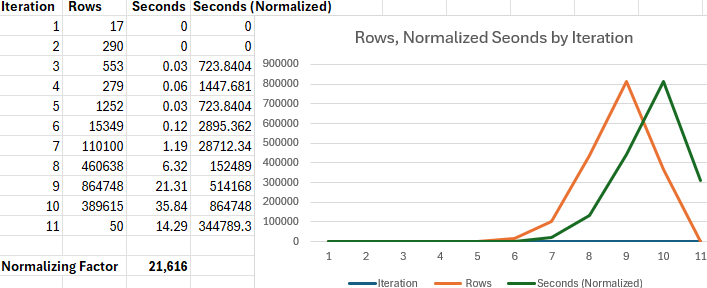
The graph shows that no significant time is taken until the rows exceeds about 100,000 in iteration 7, and shows that the times rise in proportion to the rows at the prior iteration. This makes sense because the driving row set at each iteration is the set of paths returned at the prior iteration.
Execution Plans
↑ 3 PL/SQL-Driven Solution Methods: Performance
↓ Pop_Table_Recurse
↓ Pop_Table_Iterate
↓ Array_Recurse
↓ Array_Iterate
Execution plans were taken from the SELECT statement at the 10’th iteration for the England dataset, where the code timing results showed most time was spent. The plans are generally simpler than those in the previous article from recursive SQL solution methods, with no join to an item running sums collection in particular.
The plans were gathered automatically within the code, by means of adding a hint to the query and then making a call to a wrapper utility function, Utils.Get_XPlan, Oracle PL/SQL General Utilities Module. For example:
Hint
/*+ gather_plan_statistics INSERT_PATHS */
Utility Function Calls
At the 10’th iteration the most recent plan with the marker INSERT_PATHS is retrieved to an array of strings by Utils.Get_XPlan, and written out by Utils.W.
IF p_iter = 10 THEN
Utils.W(Utils.Get_XPlan(p_sql_marker => 'INSERT_PATHS'));
END IF;
Pop_Table_Recurse
The code timing line for the 10’th iteration on the England dataset with KEEP_NUM = 0 and MIN_VALUE = 1952 was:
Timer Elapsed CPU Calls Ela/Call CPU/Call
------------------------ ---------- ---------- ---------- ------------- -------------
Insert paths 10 (389615) 36.37 36.03 1 36.37100 36.03000
The plan shows a nested loops join between PATHS and SYS_IOT_TOP_165264, which is the index on the index-organized table, ITEMS_RANKED, and is accessed via an index range scan.
Plan hash value: 2684864324
----------------------------------------------------------------------------------------------------------------------------------------------
| Id | Operation | Name | Starts | E-Rows | A-Rows | A-Time | Buffers | OMem | 1Mem | Used-Mem | Used-Tmp|
----------------------------------------------------------------------------------------------------------------------------------------------
| 0 | INSERT STATEMENT | | 1 | | 0 |00:00:36.16 | 922K| | | | |
| 1 | LOAD TABLE CONVENTIONAL | PATHS | 1 | | 0 |00:00:36.16 | 922K| | | | |
|* 2 | VIEW | | 1 | 1 | 389K|00:00:35.94 | 890K| | | | |
| 3 | WINDOW SORT | | 1 | 1 | 389K|00:00:35.76 | 890K| 82M| 3117K| 73M (0)| |
| 4 | NESTED LOOPS | | 1 | 1 | 389K|00:00:12.54 | 890K| | | | |
|* 5 | TABLE ACCESS FULL | PATHS | 1 | 1 | 864K|00:00:00.15 | 16167 | | | | |
|* 6 | INDEX RANGE SCAN | SYS_IOT_TOP_177213 | 864K| 1 | 389K|00:00:32.73 | 874K| | | | |
----------------------------------------------------------------------------------------------------------------------------------------------
Predicate Information (identified by operation id):
---------------------------------------------------
2 - filter(("PATH_RNK"<=:B7 OR :B7=0))
5 - filter("TRW"."LEV"<:B1)
6 - access("IRK"."ITEM_RNK">="TRW"."ITEM_RNK"+1)
filter(("TRW"."TOT_PRICE"+"IRK"."ITEM_PRICE"+:B5<=:B4 AND "TRW"."TOT_VALUE"+"IRK"."ITEM_VALUE"+:B3>=:B2 AND
"IRK"."ITEM_RNK"<="IRK"."N_ITEMS"-(:B1-"TRW"."LEV"-1) AND "IRK"."MAX_ITEMS">=CASE "IRK"."CAT_ID" WHEN "TRW"."CAT_ID" THEN
"TRW"."SAME_CATS"+1 ELSE 1 END AND "IRK"."MIN_REMAIN"<=:B1-("TRW"."LEV"+1)+LEAST(CASE "IRK"."CAT_ID" WHEN "TRW"."CAT_ID" THEN
"TRW"."SAME_CATS"+1 ELSE 1 END ,"IRK"."MIN_ITEMS") AND ("IRK"."CAT_ID"="TRW"."CAT_ID" OR "TRW"."SAME_CATS">="TRW"."MIN_ITEMS") AND
("IRK"."CAT_ID"="TRW"."CAT_ID" OR "IRK"."CAT_ID"=NVL("TRW"."NEXT_CAT_ID","IRK"."CAT_ID"))))
Note
-----
- dynamic statistics used: dynamic sampling (level=2)
Pop_Table_Iterate
The code timing line for the 10’th iteration on the England dataset with KEEP_NUM = 0 and MIN_VALUE = 1952 was:
Timer Elapsed CPU Calls Ela/Call CPU/Call
------------------------ ---------- ---------- ---------- ------------- -------------
Insert paths 10 (389615) 35.84 35.50 1 35.83500 35.50000
The plan here is the same as for Pop_Table_Recurse.
Plan hash value: 2684864324
----------------------------------------------------------------------------------------------------------------------------------------------
| Id | Operation | Name | Starts | E-Rows | A-Rows | A-Time | Buffers | OMem | 1Mem | Used-Mem | Used-Tmp|
----------------------------------------------------------------------------------------------------------------------------------------------
| 0 | INSERT STATEMENT | | 1 | | 0 |00:00:35.61 | 919K| | | | |
| 1 | LOAD TABLE CONVENTIONAL | PATHS | 1 | | 0 |00:00:35.61 | 919K| | | | |
|* 2 | VIEW | | 1 | 1 | 389K|00:00:35.38 | 889K| | | | |
| 3 | WINDOW SORT | | 1 | 1 | 389K|00:00:35.20 | 889K| 82M| 3117K| 73M (0)| |
| 4 | NESTED LOOPS | | 1 | 1 | 389K|00:00:07.07 | 889K| | | | |
|* 5 | TABLE ACCESS FULL | PATHS | 1 | 1 | 864K|00:00:00.13 | 15142 | | | | |
|* 6 | INDEX RANGE SCAN | SYS_IOT_TOP_177213 | 864K| 1 | 389K|00:00:32.22 | 874K| | | | |
----------------------------------------------------------------------------------------------------------------------------------------------
Predicate Information (identified by operation id):
---------------------------------------------------
2 - filter(("PATH_RNK"<=:B7 OR :B7=0))
5 - filter("TRW"."LEV"<:B1)
6 - access("IRK"."ITEM_RNK">="TRW"."ITEM_RNK"+1)
filter(("TRW"."TOT_PRICE"+"IRK"."ITEM_PRICE"+:B5<=:B4 AND "TRW"."TOT_VALUE"+"IRK"."ITEM_VALUE"+:B3>=:B2 AND
"IRK"."ITEM_RNK"<="IRK"."N_ITEMS"-(:B1-"TRW"."LEV"-1) AND "IRK"."MAX_ITEMS">=CASE "IRK"."CAT_ID" WHEN "TRW"."CAT_ID" THEN
"TRW"."SAME_CATS"+1 ELSE 1 END AND "IRK"."MIN_REMAIN"<=:B1-("TRW"."LEV"+1)+LEAST(CASE "IRK"."CAT_ID" WHEN "TRW"."CAT_ID" THEN
"TRW"."SAME_CATS"+1 ELSE 1 END ,"IRK"."MIN_ITEMS") AND ("IRK"."CAT_ID"="TRW"."CAT_ID" OR "TRW"."SAME_CATS">="TRW"."MIN_ITEMS") AND
("IRK"."CAT_ID"="TRW"."CAT_ID" OR "IRK"."CAT_ID"=NVL("TRW"."NEXT_CAT_ID","IRK"."CAT_ID"))))
Note
-----
- dynamic statistics used: dynamic sampling (level=2)
Array_Recurse
The code timing line for the 10’th iteration on the England dataset with KEEP_NUM = 0 and MIN_VALUE = 1952 was:
Timer Elapsed CPU Calls Ela/Call CPU/Call
------------------------ ---------- ---------- ---------- ------------- -------------
Recurse level: 10 (389615) 63.21 62.56 1 63.21000 62.56000
The plan here does not include an INSERT, but is more complicated than for Pop_Table_* solution methods, with merge join and two sort joins, and the time used is dignificantly larger.
Plan hash value: 4226761357
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------
| Id | Operation | Name | Starts | E-Rows | A-Rows | A-Time | Buffers | Reads | Writes | OMem | 1Mem | Used-Mem | Used-Tmp|
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------
| 0 | SELECT STATEMENT | | 1 | | 389K|00:01:51.12 | 75 | 18012 | 18012 | | | | |
|* 1 | VIEW | | 1 | 1 | 389K|00:01:51.12 | 75 | 18012 | 18012 | | | | |
| 2 | WINDOW SORT | | 1 | 1 | 389K|00:01:50.88 | 75 | 18012 | 18012 | 80M| 3082K| 71M (0)| |
| 3 | MERGE JOIN | | 1 | 1 | 389K|00:00:54.06 | 75 | 18012 | 18012 | | | | |
| 4 | SORT JOIN | | 1 | 408 | 864K|00:00:49.43 | 68 | 18012 | 18012 | 104M| 3482K| 92M (0)| |
|* 5 | COLLECTION ITERATOR PICKLER FETCH| ARRAY_RECURSE | 1 | 408 | 864K|00:00:55.05 | 68 | 18012 | 18012 | | | | |
|* 6 | FILTER | | 864K| | 389K|00:00:57.04 | 7 | 0 | 0 | | | | |
|* 7 | SORT JOIN | | 864K| 560 | 193M|00:00:34.17 | 7 | 0 | 0 | 124K| 124K| 110K (0)| |
| 8 | INDEX FAST FULL SCAN | SYS_IOT_TOP_177213 | 1 | 560 | 560 |00:00:00.01 | 7 | 0 | 0 | | | | |
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Predicate Information (identified by operation id):
---------------------------------------------------
1 - filter(("PATH_RNK"<=:B8 OR :B8=0))
5 - filter(VALUE(KOKBF$)<:B3)
6 - filter((VALUE(KOKBF$)+"IRK"."ITEM_PRICE"+:B7<=:B6 AND VALUE(KOKBF$)+"IRK"."ITEM_VALUE"+:B5>=:B4 AND "IRK"."ITEM_RNK"<="IRK"."N_ITEMS"-(:B3-VALUE(KOKBF$)-1)
AND ("IRK"."CAT_ID"=VALUE(KOKBF$) OR "IRK"."CAT_ID"=NVL(VALUE(KOKBF$),"IRK"."CAT_ID")) AND "IRK"."MAX_ITEMS">=CASE "IRK"."CAT_ID" WHEN VALUE(KOKBF$) THEN
VALUE(KOKBF$)+1 ELSE 1 END AND ("IRK"."CAT_ID"=VALUE(KOKBF$) OR VALUE(KOKBF$)>=VALUE(KOKBF$)) AND "IRK"."MIN_REMAIN"<=:B3-(VALUE(KOKBF$)+1)+LEAST(CASE
"IRK"."CAT_ID" WHEN VALUE(KOKBF$) THEN VALUE(KOKBF$)+1 ELSE 1 END ,"IRK"."MIN_ITEMS")))
7 - access("IRK"."ITEM_RNK">=VALUE(KOKBF$)+1)
filter("IRK"."ITEM_RNK">=VALUE(KOKBF$)+1)
Note
-----
- dynamic statistics used: dynamic sampling (level=2)
Array_Iterate
The code timing line for the 10’th iteration on the England dataset with KEEP_NUM = 0 and MIN_VALUE = 1952 was:
Timer Elapsed CPU Calls Ela/Call CPU/Call
-------------------- ---------- ---------- ---------- ------------- -------------
Insert 10 (1) 51.58 50.55 1 51.57900 50.55000
The plan here is closer to that of the table methods, although somewhat slower, but faster than for Array_Recurse.
Plan hash value: 1740109178
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------
| Id | Operation | Name | Starts | E-Rows | A-Rows | A-Time | Buffers | Reads | Writes | OMem | 1Mem | Used-Mem | Used-Tmp|
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------
| 0 | SELECT STATEMENT | | 1 | | 389K|00:00:51.12 | 874K| 9797 | 9797 | | | | |
|* 1 | VIEW | | 1 | 1 | 389K|00:00:51.12 | 874K| 9797 | 9797 | | | | |
| 2 | WINDOW SORT | | 1 | 1 | 389K|00:00:50.87 | 874K| 9797 | 9797 | 86M| 3186K| 5045K (1)| 77M|
| 3 | NESTED LOOPS | | 1 | 1 | 389K|00:00:06.91 | 874K| 0 | 0 | | | | |
|* 4 | COLLECTION ITERATOR PICKLER FETCH| | 1 | 1 | 864K|00:00:01.10 | 0 | 0 | 0 | | | | |
|* 5 | INDEX RANGE SCAN | SYS_IOT_TOP_177213 | 864K| 1 | 389K|00:00:45.69 | 874K| 0 | 0 | | | | |
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Predicate Information (identified by operation id):
---------------------------------------------------
1 - filter(("PATH_RNK"<=:B7 OR :B7=0))
4 - filter(VALUE(KOKBF$)<:B2)
5 - access("IRK"."ITEM_RNK">=VALUE(KOKBF$)+1)
filter((VALUE(KOKBF$)+"IRK"."ITEM_PRICE"+:B6<=:B5 AND VALUE(KOKBF$)+"IRK"."ITEM_VALUE"+:B4>=:B3 AND "IRK"."ITEM_RNK"<="IRK"."N_ITEMS"-(:B2-VALUE(KOKBF$)-1)
AND ("IRK"."CAT_ID"=VALUE(KOKBF$) OR "IRK"."CAT_ID"=NVL(VALUE(KOKBF$),"IRK"."CAT_ID")) AND "IRK"."MAX_ITEMS">=CASE "IRK"."CAT_ID" WHEN VALUE(KOKBF$) THEN
VALUE(KOKBF$)+1 ELSE 1 END AND ("IRK"."CAT_ID"=VALUE(KOKBF$) OR VALUE(KOKBF$)>=VALUE(KOKBF$)) AND "IRK"."MIN_REMAIN"<=:B2-(VALUE(KOKBF$)+1)+LEAST(CASE
"IRK"."CAT_ID" WHEN VALUE(KOKBF$) THEN VALUE(KOKBF$)+1 ELSE 1 END ,"IRK"."MIN_ITEMS")))
Note
-----
- dynamic statistics used: dynamic sampling (level=2)
4 Tuning Memory Usage
↑ Contents
↓ Path Columns
↓ Category Path Compacting
↓ Item Path Compacting
↓ Item and Category Path Compacting Combined
↓ Results Comparison
In the section on performance we saw that the Table methods performed slightly better than the Array methods, and appear more robust in terms of cardinality estimation. Let’s take the best performing (by a small margin) Table / Iterate method and see whether we can tune memory usage and see what effect that may have on performance.
Path Columns
Here is the execution plan steps for the England dataset on the parameter pair: KEEP_NUM = 0, MIN_VALUE = 1952.
Plan hash value: 2684864324
----------------------------------------------------------------------------------------------------------------------------------------------
| Id | Operation | Name | Starts | E-Rows | A-Rows | A-Time | Buffers | OMem | 1Mem | Used-Mem | Used-Tmp|
----------------------------------------------------------------------------------------------------------------------------------------------
| 0 | INSERT STATEMENT | | 1 | | 0 |00:00:35.61 | 919K| | | | |
| 1 | LOAD TABLE CONVENTIONAL | PATHS | 1 | | 0 |00:00:35.61 | 919K| | | | |
|* 2 | VIEW | | 1 | 1 | 389K|00:00:35.38 | 889K| | | | |
| 3 | WINDOW SORT | | 1 | 1 | 389K|00:00:35.20 | 889K| 82M| 3117K| 73M (0)| |
| 4 | NESTED LOOPS | | 1 | 1 | 389K|00:00:07.07 | 889K| | | | |
|* 5 | TABLE ACCESS FULL | PATHS | 1 | 1 | 864K|00:00:00.13 | 15142 | | | | |
|* 6 | INDEX RANGE SCAN | SYS_IOT_TOP_177213 | 864K| 1 | 389K|00:00:32.22 | 874K| | | | |
----------------------------------------------------------------------------------------------------------------------------------------------
Predicate Information (identified by operation id):
---------------------------------------------------
2 - filter(("PATH_RNK"<=:B7 OR :B7=0))
5 - filter("TRW"."LEV"<:B1)
6 - access("IRK"."ITEM_RNK">="TRW"."ITEM_RNK"+1)
filter(("TRW"."TOT_PRICE"+"IRK"."ITEM_PRICE"+:B5<=:B4 AND "TRW"."TOT_VALUE"+"IRK"."ITEM_VALUE"+:B3>=:B2 AND
"IRK"."ITEM_RNK"<="IRK"."N_ITEMS"-(:B1-"TRW"."LEV"-1) AND "IRK"."MAX_ITEMS">=CASE "IRK"."CAT_ID" WHEN "TRW"."CAT_ID" THEN
"TRW"."SAME_CATS"+1 ELSE 1 END AND "IRK"."MIN_REMAIN"<=:B1-("TRW"."LEV"+1)+LEAST(CASE "IRK"."CAT_ID" WHEN "TRW"."CAT_ID" THEN
"TRW"."SAME_CATS"+1 ELSE 1 END ,"IRK"."MIN_ITEMS") AND ("IRK"."CAT_ID"="TRW"."CAT_ID" OR "TRW"."SAME_CATS">="TRW"."MIN_ITEMS") AND
("IRK"."CAT_ID"="TRW"."CAT_ID" OR "IRK"."CAT_ID"=NVL("TRW"."NEXT_CAT_ID","IRK"."CAT_ID"))))
Note
-----
- dynamic statistics used: dynamic sampling (level=2)
Much of the work appears to be done in step 6, the index range scan of SYS_IOT_TOP_165264, which is the index on the index-organised table, ITEMS_RANKED in the nested loops join from the PATHS table, where 864K starts results in 389K rows, with an A-Time of 00:00:32.22, and Buffers of 874K.
The index-organized table ITEMS_RANKED is created thus:
CREATE TABLE items_ranked (
item_id VARCHAR2(3),
cat_id VARCHAR2(5),
item_price INTEGER,
item_value INTEGER,
min_items INTEGER,
max_items INTEGER,
min_remain INTEGER,
next_cat_id VARCHAR2(5),
item_rnk INTEGER PRIMARY KEY,
n_items INTEGER
)
ORGANIZATION INDEX
The temporary table PATHS is created thus:
CREATE GLOBAL TEMPORARY TABLE paths (
path_rnk INTEGER,
item_rnk INTEGER,
lev INTEGER,
tot_price INTEGER,
tot_value INTEGER,
cat_id VARCHAR2(5),
next_cat_id VARCHAR2(5),
same_cats INTEGER,
min_items INTEGER,
cats_path VARCHAR2(50),
path VARCHAR2(50)
)
ON COMMIT DELETE ROWS
There are two columns, cats_path and path, in the PATHS table that accumulate different kinds of path, concatenating a string value to the current path values at each iteration. It seemed possible that we might be able to reduce the storage associated with these paths, and that processing smaller amounts of data could reduce the execution times.
Category Path Compacting
↑ 4 Tuning Memory Usage
↓ A Compact Method for Representing Category Path
↓ Procedure pop_Items_Ranked_Base
↓ Results
A Compact Method for Representing Category Path
↑ Category Path Compacting
↓ Category Numbers via Number Bases
↓ Revised Data Model
Category Numbers via Number Bases
↑ A Compact Method for Representing Category Path
The column CATS_PATH is used to store the category id path through the iterations. This path is used to partition the path ranking that is used to filter out lower valued paths according to the KEEP_NUM value:
WHERE path_rnk <= g_keep_num OR g_keep_num = 0;
The path rank is calculated as follows:
SELECT Row_Number() OVER (PARTITION BY trw.cats_path || irk.cat_id
ORDER BY trw.tot_value + irk.item_value DESC,
trw.tot_price + irk.item_price) path_rnk
The reason for this partitioning is that there are upper and lower limits on the total numbers of items in each category allowed, and if we calculate the ranks globally paths may be excluded early on value grounds that might be required to meet the category limits. This reduces the effectiveness of the approximative KEEP_NUM parameter as it would have to be kept higher than would otherwise be necessary.
However, although we need to maintain category based partitioning, there is another, more compact, way of achieving this. Firstly, note that we only need the numbers of items in each category, not the order they occur in the iteration scheme. Secondly, note that there are a relatively small number of categories, and each has a small maximum limit (which can’t of course be larger than the sequence length).
If we have M categories in a given order, then we can represent the category path by a sequence of integers indicating the numbers of items in each category:
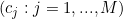
If we have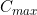 
= the maximum number of items possible in any category, then we can consider the sequence to represent a single number in the number base 
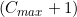. This can be represented as a decimal integer by the following sum:
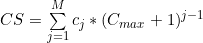
Remember that our only use of the category path is in the partitioning clause, and this unique identifier for that path is sufficient for the purpose. Furthermore, we can replace the string category identifier with the integer value:
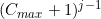
Then at each iteration we can simply add to the integer representing the category path this new integer category identifier, which we’ll call cat_base_id.
Now instead of accumulating the category path string, cats_path, as:
trw.cats_path || irk.cat_id cats_path
we can calculate cat_base_sum as the integer value:
trw.cat_base_sum + irk.cat_base_id cat_base_sum
and the path rank calculation becomes:
SELECT Row_Number() OVER (PARTITION BY trw.cat_base_sum + irk.cat_base_id
ORDER BY trw.tot_value + irk.item_value DESC,
trw.tot_price + irk.item_price) path_rnk
Revised Data Model
↑ A Compact Method for Representing Category Path
The revised data model uses a sequence for the unique identifier for the records in the new links table, and the SQL for the new and updated objects is given below.
CREATE TABLE items_ranked_base (
item_id VARCHAR2(3),
cat_base_id INTEGER,
item_price INTEGER,
item_value INTEGER,
min_items INTEGER,
max_items INTEGER,
min_remain INTEGER,
next_cat_base_id INTEGER,
item_rnk INTEGER PRIMARY KEY,
n_items INTEGER
)
ORGANIZATION INDEX
/
CREATE GLOBAL TEMPORARY TABLE paths_base (
path_rnk INTEGER,
item_rnk INTEGER,
lev INTEGER,
tot_price INTEGER,
tot_value INTEGER,
cat_base_id INTEGER,
next_cat_base_id INTEGER,
same_cats INTEGER,
min_items INTEGER,
cat_base_sum INTEGER,
path VARCHAR2(50)
)
ON COMMIT DELETE ROWS
/
Procedure pop_Items_Ranked_Base
The procedure pop_Items_Ranked is replaced by a new version using the integer identifiers:
PROCEDURE pop_Items_Ranked_Base IS
BEGIN
DELETE items_ranked_based;
INSERT INTO items_ranked_base
WITH cat_base_ids AS (
SELECT id, Power (max_max_items + 1, cat_rnk - 2) cat_base_id
FROM category_rsums_v
)
SELECT itm.id,
cbi.cat_base_id,
itm.item_price,
itm.item_value,
crs.min_items,
crs.max_items,
crs.min_remain,
cbi_n.cat_base_id next_cat_base_id,
Row_Number() OVER (ORDER BY crs.cat_rnk, itm.item_value DESC, itm.id),
Count(*) OVER ()
FROM items itm
JOIN category_rsums_v crs
ON crs.id = itm.category_id
JOIN cat_base_ids cbi
ON cbi.id = itm.category_id
LEFT JOIN cat_base_ids cbi_n
ON cbi_n.id = crs.next_cat_id;
END pop_Items_Ranked_Base;
Results
↑ Category Path Compacting
↓ Timings
↓ Execution Plans
Timings
Here are the times taken on the England dataset with KEEP_NUM = 0 and MIN_VALUE = 1952:
Timer Elapsed CPU
---------------------- ---------- ----------
Pop_Table_Iterate 80.87 78.89
Pop_Table_Iterate_Base 87.28 82.65
The new method has used slightly more time overall. The code timing line for the 10’th iteration were:
Timer Elapsed CPU Calls Ela/Call CPU/Call
----------------------------- ---------- ---------- ---------- ------------- -------------
Insert paths 10 (389615) 35.84 35.50 1 35.83500 35.50000
Insert paths_Base 10 (389615) 42.01 39.00 1 42.00700 39.00000
The revised insert has taken a bit more elapsed time than the other one. Let’s see how the execution plan has changed.
Execution Plans
↑ Results
↓ Pop_Table_Iterate
↓ Pop_Table_Iterate_Base
Pop_Table_Iterate
Plan hash value: 2684864324
----------------------------------------------------------------------------------------------------------------------------------------------
| Id | Operation | Name | Starts | E-Rows | A-Rows | A-Time | Buffers | OMem | 1Mem | Used-Mem | Used-Tmp|
----------------------------------------------------------------------------------------------------------------------------------------------
| 0 | INSERT STATEMENT | | 1 | | 0 |00:00:35.61 | 919K| | | | |
| 1 | LOAD TABLE CONVENTIONAL | PATHS | 1 | | 0 |00:00:35.61 | 919K| | | | |
|* 2 | VIEW | | 1 | 1 | 389K|00:00:35.38 | 889K| | | | |
| 3 | WINDOW SORT | | 1 | 1 | 389K|00:00:35.20 | 889K| 82M| 3117K| 73M (0)| |
| 4 | NESTED LOOPS | | 1 | 1 | 389K|00:00:07.07 | 889K| | | | |
|* 5 | TABLE ACCESS FULL | PATHS | 1 | 1 | 864K|00:00:00.13 | 15142 | | | | |
|* 6 | INDEX RANGE SCAN | SYS_IOT_TOP_177213 | 864K| 1 | 389K|00:00:32.22 | 874K| | | | |
----------------------------------------------------------------------------------------------------------------------------------------------
Predicate Information (identified by operation id):
---------------------------------------------------
2 - filter(("PATH_RNK"<=:B7 OR :B7=0))
5 - filter("TRW"."LEV"<:B1)
6 - access("IRK"."ITEM_RNK">="TRW"."ITEM_RNK"+1)
filter(("TRW"."TOT_PRICE"+"IRK"."ITEM_PRICE"+:B5<=:B4 AND "TRW"."TOT_VALUE"+"IRK"."ITEM_VALUE"+:B3>=:B2 AND
"IRK"."ITEM_RNK"<="IRK"."N_ITEMS"-(:B1-"TRW"."LEV"-1) AND "IRK"."MAX_ITEMS">=CASE "IRK"."CAT_ID" WHEN "TRW"."CAT_ID" THEN
"TRW"."SAME_CATS"+1 ELSE 1 END AND "IRK"."MIN_REMAIN"<=:B1-("TRW"."LEV"+1)+LEAST(CASE "IRK"."CAT_ID" WHEN "TRW"."CAT_ID" THEN
"TRW"."SAME_CATS"+1 ELSE 1 END ,"IRK"."MIN_ITEMS") AND ("IRK"."CAT_ID"="TRW"."CAT_ID" OR "TRW"."SAME_CATS">="TRW"."MIN_ITEMS") AND
("IRK"."CAT_ID"="TRW"."CAT_ID" OR "IRK"."CAT_ID"=NVL("TRW"."NEXT_CAT_ID","IRK"."CAT_ID"))))
Note
-----
- dynamic statistics used: dynamic sampling (level=2)
Pop_Table_Iterate_Base
Plan hash value: 2131628056
----------------------------------------------------------------------------------------------------------------------------------------------
| Id | Operation | Name | Starts | E-Rows | A-Rows | A-Time | Buffers | OMem | 1Mem | Used-Mem | Used-Tmp|
----------------------------------------------------------------------------------------------------------------------------------------------
| 0 | INSERT STATEMENT | | 1 | | 0 |00:00:41.77 | 911K| | | | |
| 1 | LOAD TABLE CONVENTIONAL | PATHS_BASE | 1 | | 0 |00:00:41.77 | 911K| | | | |
|* 2 | VIEW | | 1 | 1 | 389K|00:00:41.51 | 887K| | | | |
| 3 | WINDOW SORT | | 1 | 1 | 389K|00:00:41.32 | 887K| 68M| 2869K| 61M (0)| |
| 4 | NESTED LOOPS | | 1 | 1 | 389K|00:00:08.29 | 887K| | | | |
|* 5 | TABLE ACCESS FULL | PATHS_BASE | 1 | 1 | 864K|00:00:00.20 | 12680 | | | | |
|* 6 | INDEX RANGE SCAN | SYS_IOT_TOP_177215 | 864K| 1 | 389K|00:00:37.83 | 874K| | | | |
----------------------------------------------------------------------------------------------------------------------------------------------
Predicate Information (identified by operation id):
---------------------------------------------------
2 - filter(("PATH_RNK"<=:B7 OR :B7=0))
5 - filter("TRW"."LEV"<:B1)
6 - access("IRK"."ITEM_RNK">="TRW"."ITEM_RNK"+1)
filter(("TRW"."TOT_PRICE"+"IRK"."ITEM_PRICE"+:B5<=:B4 AND "TRW"."TOT_VALUE"+"IRK"."ITEM_VALUE"+:B3>=:B2 AND
"IRK"."ITEM_RNK"<="IRK"."N_ITEMS"-(:B1-"TRW"."LEV"-1) AND "IRK"."MAX_ITEMS">=CASE "IRK"."CAT_BASE_ID" WHEN "TRW"."CAT_BASE_ID" THEN
"TRW"."SAME_CATS"+1 ELSE 1 END AND "IRK"."MIN_REMAIN"<=:B1-("TRW"."LEV"+1)+LEAST(CASE "IRK"."CAT_BASE_ID" WHEN "TRW"."CAT_BASE_ID"
THEN "TRW"."SAME_CATS"+1 ELSE 1 END ,"IRK"."MIN_ITEMS") AND ("IRK"."CAT_BASE_ID"="TRW"."CAT_BASE_ID" OR
"TRW"."SAME_CATS">="TRW"."MIN_ITEMS") AND ("IRK"."CAT_BASE_ID"="TRW"."CAT_BASE_ID" OR
"IRK"."CAT_BASE_ID"=NVL("TRW"."NEXT_CAT_BASE_ID","IRK"."CAT_BASE_ID"))))
Note
-----
- dynamic statistics used: dynamic sampling (level=2)
The new plan shows the same steps and the same numbers of E-Rows and A-Rows at each step. The numbers of Buffers have changed slightly, and all the Mem values have reduced, the largest reducing from 82M to 68M, that is by about 17%.
Item Path Compacting
↑ 4 Tuning Memory Usage
↓ A Compact Method for Representing Item Path
↓ Procedure pop_Items_Ranked_Link
↓ View PATHS_LINK_RANKED_ITEM_V
↓ View PATHS_LINK_RANKED_PATH_V
↓ Results
A Compact Method for Representing Item Path
We would like to try to achieve a similar reduction in storage as with category paths for item paths, again through bypassing the concatenated path. However, this is more difficult for item path: The equivalent of the storage method used there would be to use a binary number for items of length equal to the number of items, and this would use much more storage than the original concatenated string.
Instead we have had to adopt a more complex approach, in which we create a new temporary table to represent paths as a chain of links from a current item to a prior item, using the integer rank as the item identifier. Initially we create this against the original data model with the concatenated category path, then subsequently we’ll try a combined model.
Revised Data Model
The revised data model uses a sequence number for the unique identifier for the records in the new links table, and the SQL for the new and updated objects is given below.
CREATE SEQUENCE iln_seq START WITH 1 CACHE 1000
/
CREATE GLOBAL TEMPORARY TABLE item_links (
id INTEGER,
item_rnk INTEGER,
prior_iln_id INTEGER
)
ON COMMIT DELETE ROWS
/
CREATE TABLE items_ranked_link (
cat_id VARCHAR2(5),
item_price INTEGER,
item_value INTEGER,
min_items INTEGER,
max_items INTEGER,
min_remain INTEGER,
next_cat_id VARCHAR2(5),
item_rnk INTEGER PRIMARY KEY
)
ORGANIZATION INDEX
/
CREATE GLOBAL TEMPORARY TABLE paths_link (
path_rnk INTEGER,
item_rnk INTEGER,
lev INTEGER,
tot_price INTEGER,
tot_value INTEGER,
cat_id VARCHAR2(5),
next_cat_id VARCHAR2(5),
same_cats INTEGER,
min_items INTEGER,
cats_path VARCHAR2(50),
prior_iln_id INTEGER,
iln_id INTEGER
)
ON COMMIT DELETE ROWS
/
Procedure pop_Items_Ranked_Link
The procedure pop_Items_Ranked_Base is replaced by a new version using the integer item_rnk as item identifier:
PROCEDURE pop_Items_Ranked_Link IS
BEGIN
DELETE items_ranked_link;
INSERT INTO items_ranked_link
SELECT itm.category_id,
itm.item_price,
itm.item_value,
crs.min_items,
crs.max_items,
crs.min_remain,
crs.next_cat_id,
Row_Number() OVER (ORDER BY crs.cat_rnk, itm.item_value DESC, itm.id)
FROM items itm
JOIN category_rsums_v crs
ON crs.id = itm.category_id;
SELECT Count(*) INTO g_n_items FROM items;
END pop_Items_Ranked_Link;
View PATHS_LINK_RANKED_ITEM_V
The view PATHS_LINK_RANKED_ITEM_V uses a recursive query to retrieve the items in each of the top-ranked paths, using PATHS_LINK as the basis for the anchor branch, and joining to ITEM_LINKS in the recursive branch:
CREATE OR REPLACE VIEW paths_link_ranked_item_v AS
WITH paths_ranked AS (
SELECT iln_id, item_rnk, prior_iln_id, tot_value, tot_price,
Row_Number() OVER (ORDER BY tot_value DESC, tot_price) rnk
FROM paths_link
), rsf (iln_id, item_rnk, prior_iln_id, lev, tot_value, tot_price, rnk) AS (
SELECT iln_id, item_rnk, prior_iln_id, 0, tot_value, tot_price, rnk
FROM paths_ranked
WHERE rnk <= To_Number(SYS_Context('RECURSION_CTX', 'TOP_N'))
UNION ALL
SELECT iln.id, iln.item_rnk, iln.prior_iln_id, rsf.lev + 1,
rsf.tot_value, rsf.tot_price, rsf.rnk
FROM rsf
JOIN item_links iln
ON iln.id = rsf.prior_iln_id
WHERE iln.id > 0
), item_map AS (
SELECT itm.id item_id,
itm.category_id,
itm.item_name,
itm.item_value,
itm.item_price,
Row_Number() OVER (ORDER BY crs.cat_rnk, itm.item_value DESC, itm.id) item_rnk
FROM items itm
JOIN category_rsums_v crs
ON crs.id = itm.category_id
)
SELECT rsf.tot_value,
rsf.tot_price,
rsf.rnk,
rsf.lev,
imp.category_id,
imp.item_id,
imp.item_name,
imp.item_value,
imp.item_price
FROM rsf
JOIN items_ranked_link irk
ON irk.item_rnk = rsf.item_rnk
JOIN item_map imp
ON imp.item_rnk = irk.item_rnk
View PATHS_LINK_RANKED_PATH_V
The view PATHS_LINK_RANKED_PATH_V brings the results back to pahth level via the aggregated function ListAgg:
CREATE OR REPLACE VIEW paths_link_ranked_path_v AS
SELECT ListAgg(item_id) WITHIN GROUP (ORDER BY lev DESC) path,
tot_value,
tot_price,
rnk
FROM paths_link_ranked_item_v
GROUP BY tot_value,
tot_price,
rnk
Results
↑ Item Path Compacting
↓ Timings
↓ Execution Plan
Timings
Here are the times taken on the England dataset with KEEP_NUM = 0 and MIN_VALUE = 1952:
Timer Elapsed CPU
---------------------- ---------- ----------
Pop_Table_Iterate 80.87 78.89
Pop_Table_Iterate_Base 87.28 82.65
Pop_Table_Iterate_Link 86.37 84.77
The new method has used slightly more time overall. The code timing line for the 10’th iteration were:
Timer Elapsed CPU Calls Ela/Call CPU/Call
----------------------------- ---------- ---------- ---------- ------------- -------------
Insert paths 10 (389615) 35.84 35.50 1 35.83500 35.50000
Insert paths_Base 10 (389615) 42.01 39.00 1 42.00700 39.00000
Insert item_links 10 (864748) 0.31 0.30 1 0.31400 0.30000
Insert paths_Link 10 (389615) 36.63 36.31 1 36.63100 36.31000
The revised insert, with the new second insert, has taken about the same elapsed time as the first one. Let’s see how the execution plan has changed.
Execution Plan
Plan hash value: 441424830
----------------------------------------------------------------------------------------------------------------------------------------------
| Id | Operation | Name | Starts | E-Rows | A-Rows | A-Time | Buffers | OMem | 1Mem | Used-Mem | Used-Tmp|
----------------------------------------------------------------------------------------------------------------------------------------------
| 0 | INSERT STATEMENT | | 1 | | 0 |00:00:36.39 | 903K| | | | |
| 1 | LOAD TABLE CONVENTIONAL | PATHS_LINK | 1 | | 0 |00:00:36.39 | 903K| | | | |
| 2 | SEQUENCE | ILN_SEQ | 1 | | 389K|00:00:36.13 | 879K| | | | |
|* 3 | VIEW | | 1 | 1 | 389K|00:00:35.61 | 879K| | | | |
| 4 | WINDOW SORT | | 1 | 1 | 389K|00:00:35.41 | 879K| 68M| 2865K| 60M (0)| |
| 5 | NESTED LOOPS | | 1 | 1 | 389K|00:00:07.89 | 879K| | | | |
|* 6 | TABLE ACCESS FULL | PATHS_LINK | 1 | 1 | 864K|00:00:00.15 | 12088 | | | | |
|* 7 | INDEX RANGE SCAN | SYS_IOT_TOP_177217 | 864K| 1 | 389K|00:00:32.40 | 867K| | | | |
----------------------------------------------------------------------------------------------------------------------------------------------
Predicate Information (identified by operation id):
---------------------------------------------------
3 - filter(("PATH_RNK"<=:B8 OR :B8=0))
6 - filter("TRW"."LEV"<:B1)
7 - access("IRK"."ITEM_RNK">="TRW"."ITEM_RNK"+1 AND "IRK"."ITEM_RNK"<=:B2-(:B1-"TRW"."LEV"-1))
filter(("TRW"."TOT_PRICE"+"IRK"."ITEM_PRICE"+:B6<=:B5 AND "TRW"."TOT_VALUE"+"IRK"."ITEM_VALUE"+:B4>=:B3 AND
"IRK"."MAX_ITEMS">=CASE "IRK"."CAT_ID" WHEN "TRW"."CAT_ID" THEN "TRW"."SAME_CATS"+1 ELSE 1 END AND
"IRK"."MIN_REMAIN"<=:B1-("TRW"."LEV"+1)+LEAST(CASE "IRK"."CAT_ID" WHEN "TRW"."CAT_ID" THEN "TRW"."SAME_CATS"+1 ELSE 1 END
,"IRK"."MIN_ITEMS") AND ("IRK"."CAT_ID"="TRW"."CAT_ID" OR "TRW"."SAME_CATS">="TRW"."MIN_ITEMS") AND ("IRK"."CAT_ID"="TRW"."CAT_ID" OR
"IRK"."CAT_ID"=NVL("TRW"."NEXT_CAT_ID","IRK"."CAT_ID"))))
Note
-----
- dynamic statistics used: dynamic sampling (level=2)
The new plan shows the same steps and the same numbers of E-Rows and A-Rows at each step as for the original Pop_Table_Iterate. The numbers of Buffers have changed slightly, and all the Mem values have reduced, the largest reducing from 82M to 68M, that is by about 17%.
The changes are similar to those for Pop_Table_Iterate_Base.
Item and Category Path Compacting Combined
↑ 4 Tuning Memory Usage
↓ Affected Objects List
↓ Results
The final compacting method simply combines the changes made for the first two, so we will not describe them in detail, but just list the affected objects.
Affected Objects List
↑ Item and Category Path Compacting Combined
Tables
- PATHS_BASE_LINK
- ITEM_BASE_LINKS
- ITEMS_RANKED_BASE_LINK
Views
- PATHS_BASE_LINK_RANKED_ITEM_V
- PATHS_BASE_LINK_RANKED_PATH_V
Procedures
- pop_Items_Ranked_Base_Link
- init_Base_Link
- insert_Init_Path_Base_Link
- insert_Paths_Base_Link
- Pop_Table_Iterate_Base_Link
Results
↑ Item and Category Path Compacting Combined
↓ Timings
↓ Execution Plan
Timings
Here are the times taken on the England dataset with KEEP_NUM = 0 and MIN_VALUE = 1952:
Timer Elapsed CPU
---------------------- ---------- ----------
Pop_Table_Iterate 80.87 78.89
Pop_Table_Iterate_Base 87.28 82.65
Pop_Table_Iterate_Link 86.37 84.77
Pop_Table_Iterate_Base_Link 84.90 83.68
The new method has used slightly more time overall. The code timing line for the 10’th iteration were:
Timer Elapsed CPU Calls Ela/Call CPU/Call
----------------------------------- ---------- ---------- ---------- ------------- -------------
Insert paths 10 (389615) 35.84 35.50 1 35.83500 35.50000
Insert paths_Base 10 (389615) 42.01 39.00 1 42.00700 39.00000
Insert item_links 10 (864748) 0.31 0.30 1 0.31400 0.30000
Insert paths_Link 10 (389615) 36.63 36.31 1 36.63100 36.31000
Insert item_base_links 10 (864748) 0.30 0.30 1 0.29500 0.30000
Insert paths_base_Link 10 (389615) 37.15 36.83 1 37.14800 36.83000
The revised insert has taken about the same elapsed time as the third. Let’s see how the execution plan has changed.
Execution Plan
Plan hash value: 66749355
----------------------------------------------------------------------------------------------------------------------------------------------
| Id | Operation | Name | Starts | E-Rows | A-Rows | A-Time | Buffers | OMem | 1Mem | Used-Mem | Used-Tmp|
----------------------------------------------------------------------------------------------------------------------------------------------
| 0 | INSERT STATEMENT | | 1 | | 0 |00:00:36.92 | 895K| | | | |
| 1 | LOAD TABLE CONVENTIONAL | PATHS_BASE_LINK | 1 | | 0 |00:00:36.92 | 895K| | | | |
| 2 | SEQUENCE | IBL_SEQ | 1 | | 389K|00:00:36.66 | 877K| | | | |
|* 3 | VIEW | | 1 | 1 | 389K|00:00:36.10 | 877K| | | | |
| 4 | WINDOW SORT | | 1 | 1 | 389K|00:00:35.92 | 877K| 55M| 2592K| 48M (0)| |
| 5 | NESTED LOOPS | | 1 | 1 | 389K|00:00:08.31 | 877K| | | | |
|* 6 | TABLE ACCESS FULL | PATHS_BASE_LINK | 1 | 1 | 864K|00:00:00.13 | 9606 | | | | |
|* 7 | INDEX RANGE SCAN | SYS_IOT_TOP_177219 | 864K| 1 | 389K|00:00:33.01 | 867K| | | | |
----------------------------------------------------------------------------------------------------------------------------------------------
Predicate Information (identified by operation id):
---------------------------------------------------
3 - filter(("PATH_RNK"<=:B8 OR :B8=0))
6 - filter("TRW"."LEV"<:B1)
7 - access("IRK"."ITEM_RNK">="TRW"."ITEM_RNK"+1 AND "IRK"."ITEM_RNK"<=:B2-(:B1-"TRW"."LEV"-1))
filter(("TRW"."TOT_PRICE"+"IRK"."ITEM_PRICE"+:B6<=:B5 AND "TRW"."TOT_VALUE"+"IRK"."ITEM_VALUE"+:B4>=:B3 AND
"IRK"."MAX_ITEMS">=CASE "IRK"."CAT_BASE_ID" WHEN "TRW"."CAT_BASE_ID" THEN "TRW"."SAME_CATS"+1 ELSE 1 END AND
"IRK"."MIN_REMAIN"<=:B1-("TRW"."LEV"+1)+LEAST(CASE "IRK"."CAT_BASE_ID" WHEN "TRW"."CAT_BASE_ID" THEN "TRW"."SAME_CATS"+1 ELSE 1 END
,"IRK"."MIN_ITEMS") AND ("IRK"."CAT_BASE_ID"="TRW"."CAT_BASE_ID" OR "TRW"."SAME_CATS">="TRW"."MIN_ITEMS") AND
("IRK"."CAT_BASE_ID"="TRW"."CAT_BASE_ID" OR "IRK"."CAT_BASE_ID"=NVL("TRW"."NEXT_CAT_BASE_ID","IRK"."CAT_BASE_ID"))))
Note
-----
- dynamic statistics used: dynamic sampling (level=2)
The new plan shows the same steps and the same numbers of E-Rows and A-Rows at each step as for the original Pop_Table_Iterate. The numbers of Buffers have changed slightly, and all the Mem values have reduced, the largest reducing from 82M to 55M, that is by about 33%.
Results Comparison
We saw above that the elapsed time for the insert(s) at iteration 10 (with the largest row count) was about 36-37 seconds for all variants, except for Pop_Table_Iterate_Base, which took 42 seconds, so the compacting methods have not made a significant difference in timing. The execution plans were also very similar, with the two variants using item path compacting having an extra SEQUENCE step before the VIEW step. Only the WINDOW SORT step showed significant differences.
Here is a table extracting the right-most execution plan columns for the WINDOW SORT, using the paths table name to identify the variant:
------------------------------------------------------------------
| Paths Table | Buffers | OMem | 1Mem | Used-Mem | Used-Tmp|
------------------------------------------------------------------
| PATHS | 889K| 82M| 3117K| 73M (0)| |
| PATHS_BASE | 887K| 68M| 2869K| 61M (0)| |
| PATHS_LINK | 879K| 68M| 2865K| 60M (0)| |
| PATHS_BASE_LINK | 877K| 55M| 2592K| 48M (0)| |
------------------------------------------------------------------
The table shows that the variants with category path and item path compacted separately both show reductions in memory used, of about 17% for 0Mem. Combining the compacting methods increases the reduction to about 33%, suggesting the reductions are additive. The variants using item path compacting also show a small reduction in buffers.
As the path compacting variant solution methods did not reduce execution times, we’ll stick with the simpler original path concatenation approach in the next section.
5 Iterative Refinement Algorithms
↑ Contents
↓ Flow Diagram
↓ Iterative Refinement - Using Pop_Table_Iterate
↓ Iterative Refinement - Using Array_Recurse
↓ Iterative Refinement - Using RSF_IRK_IRS_TABS_V
The concept of iterative refinement algorithms was introduced in the third article in this series, OPICO 3: Algorithms for Item/Category Optimization: Using a combination of Value Rank Filtering and Value Bound Filtering techniques we can generate approximative solutions quickly, and refine them within a loop where the level of approximation is reduced steadily, to get the optimal solution set more quickly than with a one-level algorithm.
This section describes three implementations in PL/SQL, all using the same outer level iterative refinement algorithm, with the inner level solution method being each of:
- Table / Iterate (Pop_Table_Iterate)
- Array / Recurse (Array_Recurse)
- Recursive SQL with pre-populated temporary tables for IRK and IRS, described in the previous article (RSF_IRK_IRS_TABS_V)
The code for each implementation is shown, results are given for the Brazil and England datasets, and a code timing report is included for the England dataset that breaks down times by iteration and step, in each case.
Flow Diagram
↑ 5 Iterative Refinement Algorithms
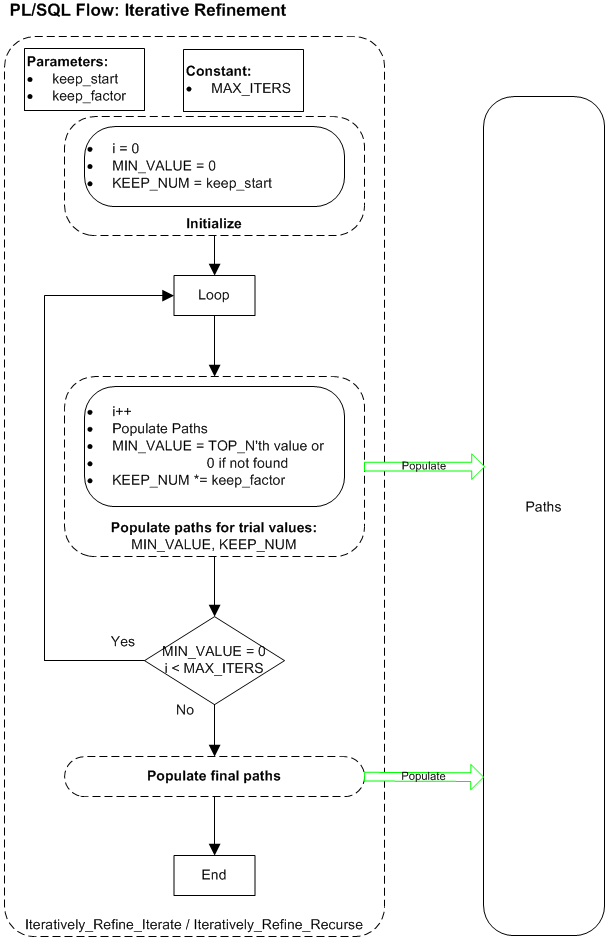
Iterative Refinement - Using Pop_Table_Iterate
↑ 5 Iterative Refinement Algorithms
↓ Code
↓ Results
The inner level solution method here was the best performing one-level method on the larger, England dataset.
Code
↑ Iterative Refinement - Using Pop_Table_Iterate
↓ PATHS Table Population and Query
↓ Procedure Iteratively_Refine_Iterate
PATHS Table Population and Query
For this solution method the PATHS temporary table is populated in a PL/SQL block, then the view that ranks the solutions is queried.
BEGIN
Item_Cat_Seqs.Iteratively_Refine_Iterate(p_keep_start => &KEEP_START,
p_keep_factor => &KEEP_FACTOR);
END;
/
PROMPT Iteratively_Refine_Iterate - path level
SELECT path,
tot_value,
tot_price,
rnk
FROM paths_ranked_v
WHERE rnk <= :TOP_N
ORDER BY rnk, tot_price
/
Procedure Iteratively_Refine_Iterate
↑ Code
The call to the procedure Pop_Table_Iterate has a boolean parameter p_do_pop_temp that is passed as TRUE only on the first iteration to ensure that the temporary tables are only populated once.
PROCEDURE Iteratively_Refine_Iterate(
p_keep_start PLS_INTEGER,
p_keep_factor PLS_INTEGER) IS
l_top_n PLS_INTEGER := recursion_Context('TOP_N');
l_do_pop_temp BOOLEAN := TRUE;
BEGIN
g_min_value := 0;
g_keep_num := p_keep_start;
FOR i IN 1..3 LOOP
Pop_Table_Iterate(p_keep_num => g_keep_num,
p_min_value => g_min_value,
p_do_pop_temp => l_do_pop_temp);
l_do_pop_temp := FALSE;
BEGIN
WITH ranking AS (
SELECT tot_value,
Row_Number() OVER (ORDER BY tot_value DESC, tot_price) rnk
FROM paths_Link
)
SELECT tot_value
INTO g_min_value
FROM ranking
WHERE rnk = l_top_n;
EXCEPTION
WHEN NO_DATA_FOUND THEN
g_min_value := 0;
END;
g_keep_num := g_keep_num * p_keep_factor;
EXIT WHEN g_min_value > 0;
END LOOP;
Pop_Table_Iterate(p_keep_num => g_keep_num,
p_min_value => g_min_value,
p_do_pop_temp => FALSE);
END Iteratively_Refine_Iterate;
Results
↑ Iterative Refinement - Using Pop_Table_Iterate
↓ Datasets Summary
↓ Code Timing - England Dataset
Datasets Summary
Both datasets were run with a KEEP_FACTOR value of 3, and exited the loop after one iteration with a MIN_VALUE found, then a final iteration was run using the KEEP_NUM of KEEP_START * 3. The table below shows the total execution times in seconds.
Dataset Elapsed CPU
------------------------- ---------- ----------
Brazil (KEEP_START = 10) 0.8 0.8
England (KEEP_START = 50) 2.3 2.2
The solution set was verified as optimal.
The combination of the Value Rank Filtering and Value Bound Filtering techniques within the iterative refinement algorithm has produced extremely large performance improvements, especially on the larger dataset.
Code Timing - England Dataset
Timer Set: Iteratively_Refine_Iterate, Constructed at 11 Jun 2024 03:35:40, written at 03:35:42
===============================================================================================
Timer Elapsed CPU Calls Ela/Call CPU/Call
---------------------------------------------- ---------- ---------- ---------- ------------- -------------
PTI 1: MIN_VALUE / KEEP_NUM = 0 / 50 1.44 1.36 1 1.43800 1.36000
SELECT 1: MIN_VALUE / KEEP_NUM = 1952 / 50 0.00 0.00 1 0.00200 0.00000
PTI (final): MIN_VALUE / KEEP_NUM = 1952 / 150 0.72 0.72 1 0.71800 0.72000
(Other) 0.00 0.00 1 0.00000 0.00000
---------------------------------------------- ---------- ---------- ---------- ------------- -------------
Total 2.16 2.08 4 0.53950 0.52000
---------------------------------------------- ---------- ---------- ---------- ------------- -------------
[Timer timed (per call in ms): Elapsed: 0.00877, CPU: 0.00877]
The code timing table shows that the initial iteration, with MIN_VALUE = 0 and KEEP_NUM = 50 takes 1.4 seconds, and finds a new MIN_VALUE of 1952, while the final iteration with MIN_VALUE = 1952 and KEEP_NUM = 150 takes 0.7 seconds.
The difference in times between the two iterations is due to the different values of the filtering parameters: The positive MIN_VALUE on the second allows faster execution even with the KEEP_NUM parameter 3 times larger.
Iterative Refinement - Using Array_Recurse
↑ 5 Iterative Refinement Algorithms
↓ Code
↓ Results
The inner level solution method here was the worst performing one-level PL/SQL-driven method on the larger, England dataset.
Code
↑ Iterative Refinement - Using Array_Recurse
↓ View ITERATIVELY_REFINE_RECURSE_V
↓ Initialization and Query
↓ Procedure Init_Loop
↓ Function Iteratively_Refine_Recurse
View ITERATIVELY_REFINE_RECURSE_V
This view returns the records from the PL/SQL function Iteratively_Refine_Recurse, with a ranking function.
CREATE OR REPLACE VIEW iteratively_refine_recurse_v AS
SELECT path,
tot_value,
tot_price,
Row_Number() OVER (ORDER BY tot_value DESC, tot_price) rnk
FROM TABLE(Item_Cat_Seqs.Iteratively_Refine_Recurse)
/
Initialization and Query
Since the view that ranks the solutions calls the PL/SQL function Iteratively_Refine_Recurse, we need to populate the ITEMS_RANKED temporary table in advance, to avoid the Oracle error:
ORA-14551: cannot perform a DML operation inside a query
The Init_Loop procedure is therefore called in a PL/SQL block to do this, as well as some other initialization steps, before querying the view.
BEGIN
Item_Cat_Seqs.Init_Loop(p_keep_start => &KEEP_START,
p_keep_factor => &KEEP_FACTOR);
END;
/
PROMPT iteratively_refine_recurse_v - path level
SELECT path,
tot_value,
tot_price,
rnk
FROM iteratively_refine_recurse_v
WHERE rnk <= :TOP_N
ORDER BY rnk, tot_price
/
Procedure Init_Loop
PROCEDURE Init_Loop(
p_keep_start PLS_INTEGER,
p_keep_factor PLS_INTEGER) IS
BEGIN
g_max_price := recursion_Context('MAX_PRICE');
g_seq_size := recursion_Context('SEQ_SIZE');
g_keep_start := p_keep_start;
g_keep_factor := p_keep_factor;
pop_Item_Running_Sums;
pop_Items_Ranked;
END Init_Loop;
Function Iteratively_Refine_Recurse
FUNCTION Iteratively_Refine_Recurse
RETURN paths_arr PIPELINED IS
l_n_rows PLS_INTEGER := 0;
l_top_n PLS_INTEGER := recursion_Context('TOP_N');
BEGIN
g_min_value := 0;
g_keep_num := g_keep_start;
FOR i IN 1..3 LOOP
set_Globals(p_keep_num => g_keep_num,
p_min_value => g_min_value);
BEGIN
SELECT tot_value
INTO g_min_value
FROM array_recurse_v
WHERE rnk = l_top_n;
EXCEPTION
WHEN NO_DATA_FOUND THEN
g_min_value := 0;
END;
g_keep_num := g_keep_num * g_keep_factor;
EXIT WHEN g_min_value > 0;
END LOOP;
set_Globals(p_keep_num => g_keep_num,
p_min_value => g_min_value);
FOR rec IN (SELECT *
FROM TABLE(Item_Cat_Seqs.Array_Recurse)
) LOOP
PIPE ROW (rec);
l_n_rows := l_n_rows + 1;
END LOOP;
END Iteratively_Refine_Recurse;
Results
↑ Iterative Refinement - Using Array_Recurse
↓ Datasets Summary
↓ Code Timing - England Dataset
Datasets Summary
Both datasets were run with a KEEP_FACTOR value of 3, and exited the loop after one iteration with a MIN_VALUE found, then a final iteration was run using the KEEP_NUM of KEEP_START * 3. The table below shows the total execution times in seconds.
Dataset Elapsed CPU
------------------------- ---------- ----------
Brazil (KEEP_START = 10) 0.8 0.8
England (KEEP_START = 50) 2.8 2.7
The solution set was verified as optimal.
The combination of the Value Rank Filtering and Value Bound Filtering techniques within the iterative refinement algorithm has produced extremely large performance improvements, especially on the larger dataset.
Code Timing - England Dataset
Timer Set: Iteratively_Refine_Recurse, Constructed at 11 Jun 2024 03:35:37, written at 03:35:40
===============================================================================================
Timer Elapsed CPU Calls Ela/Call CPU/Call
----------------------------------------------- ---------- ---------- ---------- ------------- -------------
set_Globals 1: MIN_VALUE / KEEP_NUM = 0 / 50 0.00 0.00 1 0.00000 0.00000
SELECT 1: MIN_VALUE / KEEP_NUM = 1952 / 50 1.70 1.70 1 1.69800 1.70000
set_Globals: MIN_VALUE / KEEP_NUM = 1952 / 150 0.00 0.00 1 0.00000 0.00000
Pipe 21 rows: MIN_VALUE / KEEP_NUM = 1952 / 150 0.93 0.94 1 0.92500 0.94000
(Other) 0.00 0.00 1 0.00000 0.00000
----------------------------------------------- ---------- ---------- ---------- ------------- -------------
Total 2.62 2.64 5 0.52460 0.52800
----------------------------------------------- ---------- ---------- ---------- ------------- -------------
[Timer timed (per call in ms): Elapsed: 0.00877, CPU: 0.00789]
The code timing table shows that the initial iteration, with MIN_VALUE = 0 and KEEP_NUM = 50 takes 1.8 seconds, and finds a new MIN_VALUE of 1952, while the final iteration with MIN_VALUE = 1952 and KEEP_NUM = 150 takes 0.9 seconds.
The difference in times between the two iterations is due to the different values of the filtering parameters: The positive MIN_VALUE on the second allows faster execution even with the KEEP_NUM parameter 3 times larger.
Iterative Refinement - Using RSF_IRK_IRS_TABS_V
↑ 5 Iterative Refinement Algorithms
↓ Code
↓ Results
The inner level solution method here was the best performing one-level recursive SQL method on the larger, England dataset.
Code
↑ Iterative Refinement - Using RSF_IRK_IRS_TABS_V
↓ View ITERATIVELY_REFINE_RSF_V
↓ Initialization and Query
↓ Function Iteratively_Refine_RSF
View ITERATIVELY_REFINE_RSF_V
This view returns the records from the PL/SQL function Iteratively_Refine_RSF, with a ranking function.
CREATE OR REPLACE VIEW iteratively_refine_rsf_v AS
SELECT path,
tot_value,
tot_price,
Row_Number() OVER (ORDER BY tot_value DESC, tot_price) rnk
FROM TABLE(Item_Cat_Seqs.Iteratively_Refine_RSF)
/
Initialization and Query
Since the view that ranks the solutions calls the PL/SQL function Iteratively_Refine_RSF, we need to populate the ITEMS_RANKED temporary table in advance, as for Iteratively_Refine_Recurse, using the Init_Loop procedure.
BEGIN
Item_Cat_Seqs.Init_Loop(p_keep_start => &KEEP_START,
p_keep_factor => &KEEP_FACTOR);
END;
/
PROMPT iteratively_refine_rsf_v - path level
SELECT path,
tot_value,
tot_price,
rnk
FROM iteratively_refine_rsf_v
WHERE rnk <= :TOP_N
ORDER BY rnk, tot_price
/
Function Iteratively_Refine_RSF
FUNCTION Iteratively_Refine_RSF
RETURN paths_arr PIPELINED IS
l_n_rows PLS_INTEGER := 0;
l_top_n PLS_INTEGER := recursion_Context('TOP_N');
l_rec paths%ROWTYPE;
BEGIN
g_min_value := 0;
g_keep_num := g_keep_start;
FOR i IN 1..3 LOOP
Set_Contexts(p_keep_num => g_keep_num,
p_min_value => g_min_value);
BEGIN
SELECT tot_value
INTO g_min_value
FROM rsf_irk_irs_tabs_v
WHERE rnk = l_top_n;
EXCEPTION
WHEN NO_DATA_FOUND THEN
g_min_value := 0;
END;
g_keep_num := g_keep_num * g_keep_factor;
EXIT WHEN g_min_value > 0;
END LOOP;
Set_Contexts(p_keep_num => g_keep_num,
p_min_value => g_min_value);
FOR rec IN (SELECT *
FROM rsf_irk_irs_tabs_v
) LOOP
l_rec.path := rec.path;
l_rec.tot_value := rec.tot_value;
l_rec.tot_price := rec.tot_price;
PIPE ROW (l_rec);
l_n_rows := l_n_rows + 1;
END LOOP;
END Iteratively_Refine_RSF;
Results
↑ Iterative Refinement - Using RSF_IRK_IRS_TABS_V
↓ Datasets Summary
↓ Code Timing - England Dataset
Datasets Summary
Both datasets were run with a KEEP_FACTOR value of 3, and exited the loop after one iteration with a MIN_VALUE found, then a final iteration was run using the KEEP_NUM of KEEP_START * 3. The table below shows the total execution times in seconds.
Dataset Elapsed CPU
------------------------- ---------- ----------
Brazil (KEEP_START = 10) 0.5 0.4
England (KEEP_START = 50) 10.5 10.4
The solution set was verified as optimal.
The combination of the Value Rank Filtering and Value Bound Filtering techniques within the iterative refinement algorithm has produced extremely large performance improvements, especially on the larger dataset.
The run time is, however, considerably larger than for the PL/SQL-driven base methods.
Code Timing - England Dataset
Timer Set: Iteratively_Refine_RSF, Constructed at 11 Jun 2024 03:35:42, written at 03:35:53
===========================================================================================
Timer Elapsed CPU Calls Ela/Call CPU/Call
----------------------------------------------- ---------- ---------- ---------- ------------- -------------
SELECT 1: MIN_VALUE / KEEP_NUM = 1952 / 50 8.55 8.47 1 8.54800 8.47000
Set_Contexts: MIN_VALUE / KEEP_NUM = 1952 / 150 0.00 0.00 1 0.00000 0.00000
Pipe 20 rows: MIN_VALUE / KEEP_NUM = 1952 / 150 1.62 1.61 1 1.62100 1.61000
(Other) 0.22 0.21 1 0.21800 0.21000
----------------------------------------------- ---------- ---------- ---------- ------------- -------------
Total 10.39 10.29 4 2.59675 2.57250
----------------------------------------------- ---------- ---------- ---------- ------------- -------------
[Timer timed (per call in ms): Elapsed: 0.00877, CPU: 0.00789]
The code timing table shows that the initial iteration, with MIN_VALUE = 0 and KEEP_NUM = 50 takes 8.6 seconds, and finds a new MIN_VALUE of 1952, while the final iteration with MIN_VALUE = 1952 and KEEP_NUM = 150 takes 1.6 seconds.
The difference in times between the two iterations is due to the different values of the filtering parameters: The positive MIN_VALUE on the second allows faster execution even with the KEEP_NUM parameter 3 times larger.
6 Conclusion
↑ Contents
↓ Results
↓ Lessons Learned
To conclude this article, we will summarise the results, first for the four base PL/SQL-driven solution methods developed, then for two of them used within the iterative refinement scheme, and we’ll include the fastest recursive SQL method from the previous article for comparison; then we will note some lessons learned.
Results
↑ 6 Conclusion
↓ Base Solution Methods
↓ Iterative Refinement Solution Methods
Base Solution Methods
This table shows the different solution methods tested, and assigns a short code to each one for convenience.
| Code | Procedure / Function | Table / Array | Recurse / Iterate |
|---|---|---|---|
| PTR | Pop_Table_Recurse | Table | Recurse |
| PTI | Pop_Table_Iterate | Table | Iterate |
| ARE | Array_Recurse | Array | Recurse |
| AIT | Array_Iterate | Array | Iterate |
For comparison we will include the fastest recursive SQL solution method in the timings listed.
| Code | View | IRK Access | IRS Access | IRK/TRW-Conditions | IRS/TRW-Conditions |
|---|---|---|---|---|---|
| IIT | RSF_IRK_IRS_TABS_V - temporary tables for IRK and IRS | Table | Table | Inline | Inline |
Timings in the right hand columns are in seconds.
Brazil
| KEEP_NUM | MIN_VALUE | Solution Set | PTR | PTI | ARE | AIT | IIT |
|---|---|---|---|---|---|---|---|
| 10 | 0 | B-B (suboptimal) | 0.4 | 0.4 | 0.4 | 0.4 | 0.1 |
| 100 | 0 | B-A (optimal) | 0.6 | 0.6 | 0.6 | 0.6 | 1.1 |
| 100 | 10748 | B-A (optimal) | 0.4 | 0.4 | 0.4 | 0.4 | 0.1 |
| 0 | 10748 | B-A (optimal) | 0.4 | 0.4 | 0.4 | 0.4 | 0.1 |
England
| KEEP_NUM | MIN_VALUE | Solution Set | PTR | PTI | ARE | AIT | IIT |
|---|---|---|---|---|---|---|---|
| 50 | 0 | E-B (suboptimal) | 1 | 1 | 2 | 2 | 9 |
| 300 | 0 | E-A (optimal) | 7 | 7 | 9 | 9 | 72 |
| 300 | 1952 | E-A (optimal) | 1 | 1 | 1 | 1 | 3 |
| 0 | 1952 | E-A (optimal) | 83 | 81 | 140 | 116 | 214 |
Iterative Refinement Solution Methods
Two of the base PL/SQL methods, along with the best recursive SQL method, were used within the iterative refinement scheme, with a single pair of parameter values each, as shown below.
Timings in the right hand columns are in seconds.
| Dataset | KEEP_START | KEEP_FACTOR | Solution Set | ARE | PTI | IIT |
|---|---|---|---|---|---|---|
| Brazil | 10 | 3 | B-A (optimal) | 0.8 | 0.8 | 0.5 |
| England | 50 | 3 | E-A (optimal) | 2.8 | 2.3 | 10.5 |
Lessons Learned
We can summarise the principle points we have learned in relation to solving these problems using PL/SQL-driven solution methods, with the Value Filtering techniques:
- All variants of the PL/SQL-driven solution methods are much faster than the fastest recursive SQL method on the larger, England, dataset, across all tested pairs of the filtering parameters
- All methods return results in less than a second on the smaller, Brazil, dataset; remember that, without our
Value Filteringtechniques, we could not solve for even the smaller dataset at all - For these problems, the solution methods using a temporary table for the intermediate paths proved significantly faster than those using arrays
- Recursion seemed to be slightly slower than iteration on both array and table based solution methods
- Applying the filtering techniques within an
Iterative Refinementalgorithm has allowed us to solve for the exact optimal solution set on the larger dataset in just a couple of seconds - Finding more efficient storage methods for paths reduced reported memory usage, although not run times
In the next article, we discuss how to verify correctness of solution methods for algorithmic problems of this kind, using a number of approaches, including unit testing.