OPICO 2: SQL for Item Sequence Generation
Part 2 in a series on: Optimization Problems with Items and Categories in Oracle
The knapsack problem is a problem in combinatorial optimization: Given a set of items, each with a weight and a value, determine the number of each item to include in a collection so that the total weight is less than or equal to a given limit and the total value is as large as possible.
The knapsack problem and many other problems in combinatorial optimization require the selection of a subset of items to maximize an objective function subject to constraints. A common approach to solving these problems algorithmically involves recursively generating sequences of items of increasing length in a search for the best subset that meets the constraints.
I applied this kind of approach using SQL for a number of problems, starting in January 2013 with A Simple SQL Solution for the Knapsack Problem (SKP-1), and I wrote a summary article, Knapsacks and Networks in SQL, in December 2017 when I put the code onto GitHub, sql_demos - Brendan’s repo for interesting SQL.
This is the second in a series of eight articles that aim to provide a more formal treatment of algorithms for item sequence generation and optimization, together with practical implementations, examples and verification techniques in SQL and PL/SQL.
List of Articles
- OPICO 1: Algorithms for Item Sequence Generation
- OPICO 2: SQL for Item Sequence Generation
- OPICO 3: Algorithms for Item/Category Optimization
- OPICO 4: Recursive SQL for Item/Category Optimization
- OPICO 5: Tuning Recursive SQL for Item/Category Optimization
- OPICO 6: Mixed SQL and PL/SQL Methods for Item/Category Optimization
- OPICO 7: Verification
- OPICO 8: Automation
GitHub 
- Optimization Problems with Items and Categories in Oracle
[See README for references]
Twitter 
In the first article we reviewed methods for recursive generation of the item sequences in a generic way that is not specific to SQL or any programming language.
In the current article, we:
- discuss the structure of SQL for recursion in Oracle, with particular reference to item sequence generation
- show the SQL for generating sequences of each of the four types described in the first article, and discuss some issues encountered with cycles
- discuss the options of storing item sequences as concatenated strrings, or as nested table arrays
- demonstrate how PL/SQL can be used to implement both recursive and iterative versions with embedded SQL, using either temporary tables or arrays for path storage.
[Image by mcmurryjulie from Pixabay]
Contents
↓ 1 Item Sequence Types
↓ 2 Recursive SQL and Item Sequences
↓ 3 Item Sequence Generation by Pure SQL - Paths via String Concatenation
↓ 4 Item Sequence Generation by Pure SQL - Paths via Nested Table
↓ 5 Item Sequence Generation by Mixed SQL and PL/SQL
↓ 6 Conclusion
1 Item Sequence Types
Initially, we’ll take a simple example of sequences of length 2 from 3 items to illustrate the different types of sequence. We can depict the solution sets for these examples below:
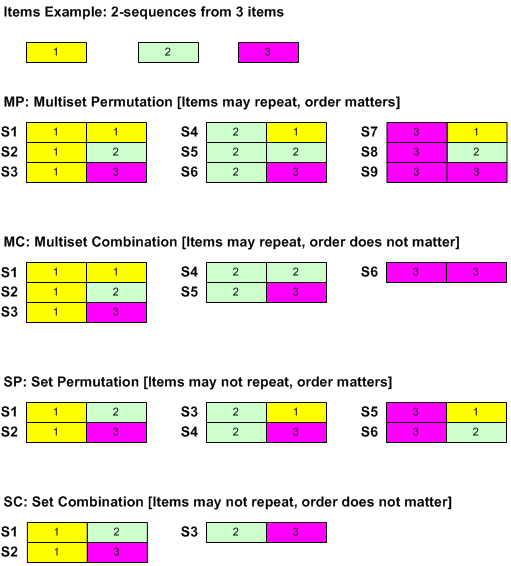
Later we’ll use a larger problem size of sequences of length 3 from 6 items, to illustrate the SQL.
2 Recursive SQL and Item Sequences
↑ Contents
↓ Recursive Query Structure
↓ Recursion Data Flow
↓ Storage of Item Sequences as Paths via String Concatenation
Here is the Oracle documentation on Recursive Subquery Factoring, and here is my own article from February 2020 on Analytic and Recursive SQL by Example.
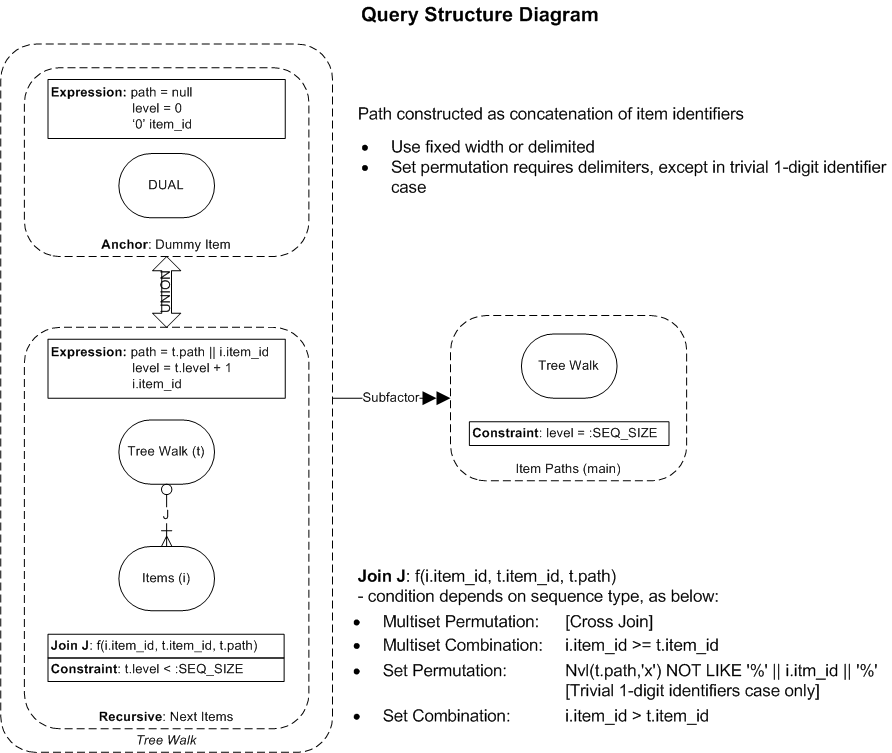
In order to generate item sequences we can take advantage of the ability of recursive subquery factors to carry forward item paths as an expression concatenating an additional item at each iteration. The query structure has the recursive factor called by a main query, where the recursive factor has the standard structure of a union between an anchor branch and a recursive branch that selects from the recursive factor itself.
The anchor branch here selects ‘0’ from dual as a kind of dummy item, with the path initialized to null. This corresponds to the choice of null set as root, as discussed in section 4 of the first article.
The recursive branch adds the next items on to the path for each record in the previous iteration, with join condition according to the type of sequence sought. The where condition terminates iteration when the desired path length is reached.
Only the main query has access to the records generated from all iterations, and in our case we need to restrict to the last iteration, which has the full length sequences in the paths. Note that we include the iteration number, as level, in the select list as well as in the where clause and this ensures that a cycle is not possible, even in the sequence types where repeated items are allowed.
Recursive Query Structure
↑ 2 Recursive SQL and Item Sequences
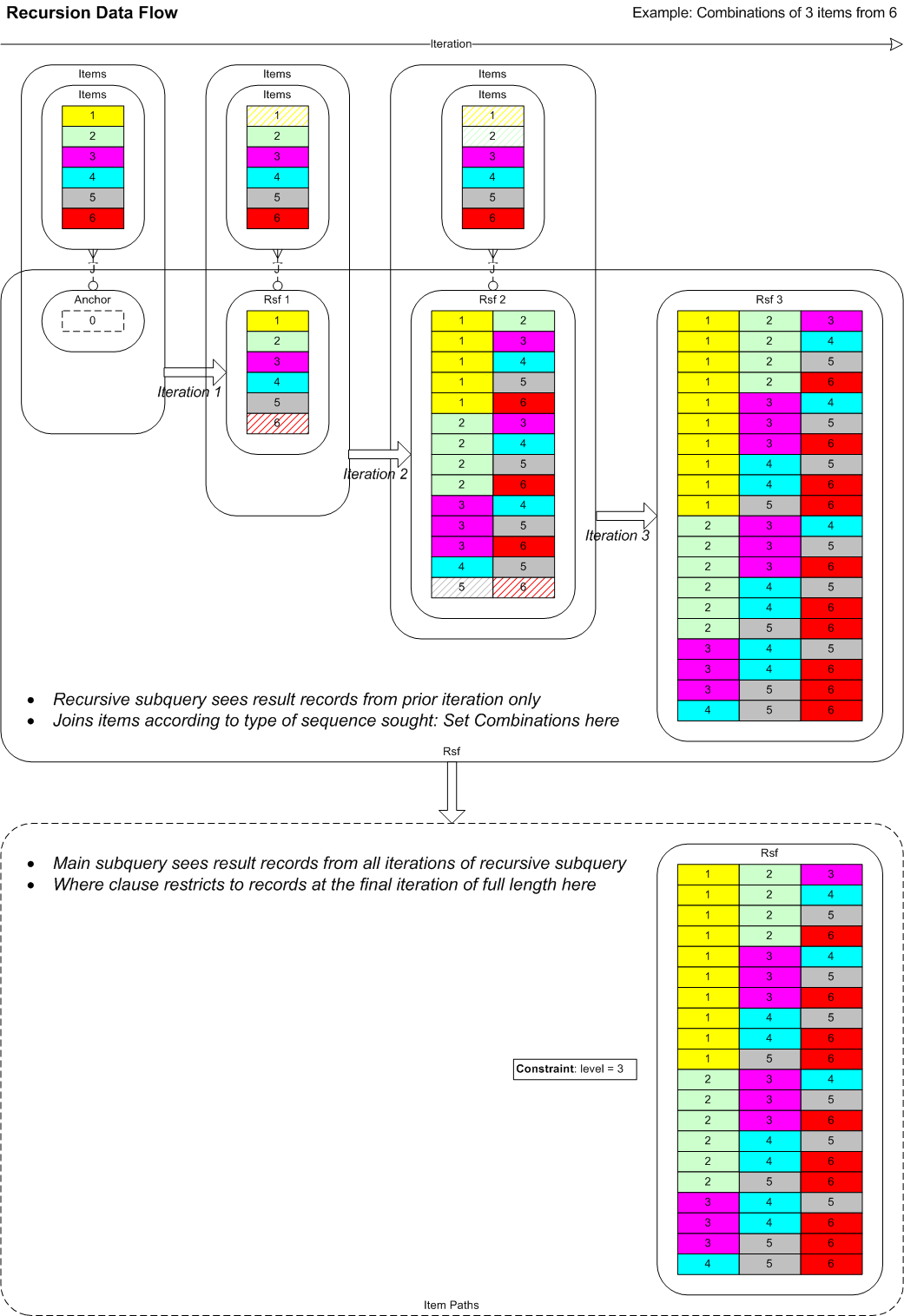
Recursion Data Flow
↑ 2 Recursive SQL and Item Sequences
In the following diagram we see how the recursion process works in the case of the simple example of finding all 3-item combination from 6 items.
Storage of Item Sequences as Paths via String Concatenation
↑ 2 Recursive SQL and Item Sequences
↓ Can we Use Nested Tables instead?
The item sequences may be stored as concatenations of item identifiers, or item paths, using either delimiters between items, or fixed length identifiers. In this case, if we want the individual items returned, we would need to split the path strings into sets of records: This is easy enough to do using standard row generation and string-splitting techniques, as we’ll see later.
Can we Use Nested Tables instead?
↑ Storage of Item Sequences as Paths via String Concatenation
It might be thought that using Oracle’s nested table type to store the item sequences in an array format would be a more elegant approach. However, the syntax for collecting and then splitting the items again does not seem particularly preferable; also, in Oracle 19.3 we found issues with Oracle finding cycles where none exist. The issues seem to have gone by Oracle 21.3, but we have retained the approach of storing the sequences as path strings, although we will also show how to implement the nested tables approach in this article.
3 Item Sequence Generation by Pure SQL - Paths via String Concatenation
↑ Contents
↓ MP: Multiset Permutation [Items may repeat, order matters]
↓ MC: Multiset Combination [Items may repeat, order does not matter]
↓ SP: Set Permutation [Items may not repeat, order matters]
↓ SC: Set Combination [Items may not repeat, order does not matter]
↓ Cycles in Recursive Subquery Factoring
In this section we show the SQL queries for generating all item sequences of a given size, SEQ_SIZE, from a set of items stored in an items table, for each of the four types of sequence discussed in the first article in the series.
The output is listed for a simple example of selecting 3 items from 6, with items having price and value. The total prices and values are accumulated through the recursion and listed here. For simplicity, the queries print the paths as a string without splitting into records.
Script on GitHub: app\item_seqs_rsf.sql
MP: Multiset Permutation [Items may repeat, order matters]
↑ 3 Item Sequence Generation by Pure SQL - Paths via String Concatenation
SQL
WITH tree_walk(item_id, lev, tot_price, tot_value, path) AS (
SELECT '0', 0, 0, 0, '' path
FROM DUAL
UNION ALL
SELECT itm.id,
trw.lev + 1,
trw.tot_price + itm.item_price,
trw.tot_value + itm.item_value,
trw.path || itm.id
FROM tree_walk trw
JOIN items itm
ON trw.lev < &SEQ_SIZE
)
SELECT path, tot_price, tot_value
FROM tree_walk
WHERE lev = &SEQ_SIZE
ORDER BY 1
Join/Where Condition
For this case we want to simply join all items with all path records from the previous iteration, which could be implemented by a CROSS JOIN in the recursive member, with the termination condition being in the WHERE clause.
CROSS JOIN items itm
WHERE trw.lev < &SEQ_SIZE
This corresponds to the condition in equation [3.1.3] from the first article, OPICO 1 / 3.1 MP: Multiset Permutation [Items may repeat, order matters].
However, in practice this results in the error:
ORA-32044: cycle detected while executing recursive WITH query
Replacing the ‘CROSS JOIN / WHERE’ construction with the ‘JOIN / ON’ construction allows the query to execute without error. This is strange since there aren’t any real cycles, as indicated by the success of the second, functionally equivalent, version. We’ll take a closer look at this later, meanwhile noting that the same issue manifests in some versions of the queries for the other item types, and we’ll use a working version in each case.
The number of sequences of type MP of size r from a set of n items =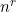 
. For example, when n = 6 and r = 3, the number of MP sequences is:
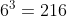
Output
Path Total Price Total Value C ---- ----------- ----------- - 111 3 3 112 4 4 113 5 5 114 3 8 115 4 6 116 5 4 121 4 4 122 5 5 123 6 6 124 4 9 125 5 7 126 6 5 131 5 5 132 6 6 133 7 7 134 5 10 135 6 8 136 7 6 141 3 8 142 4 9 143 5 10 144 3 13 145 4 11 146 5 9 151 4 6 152 5 7 153 6 8 154 4 11 155 5 9 156 6 7 161 5 4 162 6 5 163 7 6 164 5 9 165 6 7 166 7 5 211 4 4 212 5 5 213 6 6 214 4 9 215 5 7 216 6 5 221 5 5 222 6 6 223 7 7 224 5 10 225 6 8 226 7 6 231 6 6 232 7 7 233 8 8 234 6 11 235 7 9 236 8 7 241 4 9 242 5 10 243 6 11 244 4 14 245 5 12 246 6 10 251 5 7 252 6 8 253 7 9 254 5 12 255 6 10 256 7 8 261 6 5 262 7 6 263 8 7 264 6 10 265 7 8 266 8 6 311 5 5 312 6 6 313 7 7 314 5 10 315 6 8 316 7 6 321 6 6 322 7 7 323 8 8 324 6 11 325 7 9 326 8 7 331 7 7 332 8 8 333 9 9 334 7 12 335 8 10 336 9 8 341 5 10 342 6 11 343 7 12 344 5 15 345 6 13 346 7 11 351 6 8 352 7 9 353 8 10 354 6 13 355 7 11 356 8 9 361 7 6 362 8 7 363 9 8 364 7 11 365 8 9 366 9 7 411 3 8 412 4 9 413 5 10 414 3 13 415 4 11 416 5 9 421 4 9 422 5 10 423 6 11 424 4 14 425 5 12 426 6 10 431 5 10 432 6 11 433 7 12 434 5 15 435 6 13 436 7 11 441 3 13 442 4 14 443 5 15 444 3 18 445 4 16 446 5 14 451 4 11 452 5 12 453 6 13 454 4 16 455 5 14 456 6 12 461 5 9 462 6 10 463 7 11 464 5 14 465 6 12 466 7 10 511 4 6 512 5 7 513 6 8 514 4 11 515 5 9 516 6 7 521 5 7 522 6 8 523 7 9 524 5 12 525 6 10 526 7 8 531 6 8 532 7 9 533 8 10 534 6 13 535 7 11 536 8 9 541 4 11 542 5 12 543 6 13 544 4 16 545 5 14 546 6 12 551 5 9 552 6 10 553 7 11 554 5 14 555 6 12 556 7 10 561 6 7 562 7 8 563 8 9 564 6 12 565 7 10 566 8 8 611 5 4 612 6 5 613 7 6 614 5 9 615 6 7 616 7 5 621 6 5 622 7 6 623 8 7 624 6 10 625 7 8 626 8 6 631 7 6 632 8 7 633 9 8 634 7 11 635 8 9 636 9 7 641 5 9 642 6 10 643 7 11 644 5 14 645 6 12 646 7 10 651 6 7 652 7 8 653 8 9 654 6 12 655 7 10 656 8 8 661 7 5 662 8 6 663 9 7 664 7 10 665 8 8 666 9 6 216 rows selected.
MC: Multiset Combination [Items may repeat, order does not matter]
↑ 3 Item Sequence Generation by Pure SQL - Paths via String Concatenation
SQL
WITH tree_walk(item_id, lev, tot_price, tot_value, path) AS (
SELECT '0', 0, 0, 0, '' path
FROM DUAL
UNION ALL
SELECT itm.id,
trw.lev + 1,
trw.tot_price + itm.item_price,
trw.tot_value + itm.item_value,
trw.path || itm.id
FROM tree_walk trw
JOIN items itm
ON itm.id >= trw.item_id
AND trw.lev < &SEQ_SIZE
)
SELECT path, tot_price, tot_value
FROM tree_walk
WHERE lev = &SEQ_SIZE
ORDER BY 1
Join/Where Condition
JOIN items itm
ON itm.id >= trw.id
AND trw.lev < &SEQ_SIZE
In this case order is not significant, so we avoid duplication of equivalent sequences by joining items only of equal or higher rank.
This corresponds to the conditions in equation [3.2.4] from the first article, OPICO 1 / 3.2 MC: Multiset Combination [Items may repeat, order does not matter].
Output
The number of sequences of type MC of size r from a set of n items is given by the number of combinations of r items from a set of (n+r-1) items, which, using the combinatorial formula for choosing r items from (n+r-1) is:
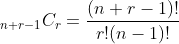
This is not so obvious, and is usually demonstrated by means of a Stars and bars diagram.
For example, when n = 6 and r = 3, the number of MC sequences is:
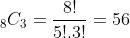
Path Total Price Total Value ---- ----------- ----------- 111 3 3 112 4 4 113 5 5 114 3 8 115 4 6 116 5 4 122 5 5 123 6 6 124 4 9 125 5 7 126 6 5 133 7 7 134 5 10 135 6 8 136 7 6 144 3 13 145 4 11 146 5 9 155 5 9 156 6 7 166 7 5 222 6 6 223 7 7 224 5 10 225 6 8 226 7 6 233 8 8 234 6 11 235 7 9 236 8 7 244 4 14 245 5 12 246 6 10 255 6 10 256 7 8 266 8 6 333 9 9 334 7 12 335 8 10 336 9 8 344 5 15 345 6 13 346 7 11 355 7 11 356 8 9 366 9 7 444 3 18 445 4 16 446 5 14 455 5 14 456 6 12 466 7 10 555 6 12 556 7 10 566 8 8 666 9 6 56 rows selected.
SP: Set Permutation [Items may not repeat, order matters]
↑ 3 Item Sequence Generation by Pure SQL - Paths via String Concatenation
SQL
WITH tree_walk(item_id, lev, tot_price, tot_value, path) AS (
SELECT '0', 0, 0, 0, '' path
FROM DUAL
UNION ALL
SELECT itm.id,
trw.lev + 1,
trw.tot_price + itm.item_price,
trw.tot_value + itm.item_value,
trw.path || itm.id
FROM tree_walk trw
JOIN items itm
ON Nvl(trw.path,'x') NOT LIKE '%' || itm.id || '%'
WHERE trw.lev < &SEQ_SIZE
)
SELECT path, tot_price, tot_value
FROM tree_walk
WHERE lev = &SEQ_SIZE
ORDER BY 1
Join/Where Condition
JOIN items itm
ON Nvl(trw.path,'x') NOT LIKE '%' || itm.id || '%'
In this case order is significant, and item repetition is not allowed, so we need to exclude duplicate items and cannot do so as simply as in the case of combinations where we can take items in order. The path string is searched using NOT LIKE with wildcards to ensure the item is not already there. In our simple example the item ids are 1-digit; for larger, more realistic data sets, you would just include delimiters in the search.
This corresponds to the conditions in equation [3.3.4] from the first article, OPICO 1 / 3.3 SP: Set Permutation [Items may not repeat, order matters].
Output
The number of sequences of type SP of size r from a set n items is given by the usual permutation formula:
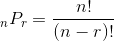
For example, when n = 6 and r = 3, the number of SP sequences is:
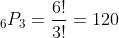
Path Total Price Total Value ---- ----------- ----------- 123 6 6 124 4 9 125 5 7 126 6 5 132 6 6 134 5 10 135 6 8 136 7 6 142 4 9 143 5 10 145 4 11 146 5 9 152 5 7 153 6 8 154 4 11 156 6 7 162 6 5 163 7 6 164 5 9 165 6 7 213 6 6 214 4 9 215 5 7 216 6 5 231 6 6 234 6 11 235 7 9 236 8 7 241 4 9 243 6 11 245 5 12 246 6 10 251 5 7 253 7 9 254 5 12 256 7 8 261 6 5 263 8 7 264 6 10 265 7 8 312 6 6 314 5 10 315 6 8 316 7 6 321 6 6 324 6 11 325 7 9 326 8 7 341 5 10 342 6 11 345 6 13 346 7 11 351 6 8 352 7 9 354 6 13 356 8 9 361 7 6 362 8 7 364 7 11 365 8 9 412 4 9 413 5 10 415 4 11 416 5 9 421 4 9 423 6 11 425 5 12 426 6 10 431 5 10 432 6 11 435 6 13 436 7 11 451 4 11 452 5 12 453 6 13 456 6 12 461 5 9 462 6 10 463 7 11 465 6 12 512 5 7 513 6 8 514 4 11 516 6 7 521 5 7 523 7 9 524 5 12 526 7 8 531 6 8 532 7 9 534 6 13 536 8 9 541 4 11 542 5 12 543 6 13 546 6 12 561 6 7 562 7 8 563 8 9 564 6 12 612 6 5 613 7 6 614 5 9 615 6 7 621 6 5 623 8 7 624 6 10 625 7 8 631 7 6 632 8 7 634 7 11 635 8 9 641 5 9 642 6 10 643 7 11 645 6 12 651 6 7 652 7 8 653 8 9 654 6 12 120 rows selected.
SC: Set Combination [Items may not repeat, order does not matter]
↑ 3 Item Sequence Generation by Pure SQL - Paths via String Concatenation
SQL
WITH tree_walk(item_id, lev, tot_price, tot_value, path) AS (
SELECT '0', 0, 0, 0, '' path
FROM DUAL
UNION ALL
SELECT itm.id,
trw.lev + 1,
trw.tot_price + itm.item_price,
trw.tot_value + itm.item_value,
trw.path || itm.id
FROM tree_walk trw
JOIN items itm
ON itm.id > trw.item_id
WHERE trw.lev < &SEQ_SIZE
)
SELECT path, tot_price, tot_value
FROM tree_walk
WHERE lev = &SEQ_SIZE
ORDER BY 1
Join/Where Condition
JOIN items itm
ON itm.id > trw.id
In this case order is not significant, so we avoid duplication of equivalent sequences by joining items only of higher rank (since item repetition is not allowed).
This corresponds to the conditions in equation [3.4.4] from the first article, OPICO 1 / 3.4 SC: Set Combination [Items may not repeat, order does not matter].
Output
The number of sequences of type SC of size r from a set n items is given by the usual combinations formula:
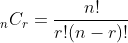
For example, when n = 6 and r = 3, the number of SC sequences is:
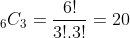
Path Total Price Total Value ---- ----------- ----------- 123 6 6 124 4 9 125 5 7 126 6 5 134 5 10 135 6 8 136 7 6 145 4 11 146 5 9 156 6 7 234 6 11 235 7 9 236 8 7 245 5 12 246 6 10 256 7 8 345 6 13 346 7 11 356 8 9 456 6 12 20 rows selected.
Cycles in Recursive Subquery Factoring
↑ 3 Item Sequence Generation by Pure SQL - Paths via String Concatenation
Script on GitHub: app\item_seqs_rsf_cycle.sql
We noted above that for the MP type, with the following join/where clause:
CROSS JOIN items itm
WHERE trw.lev < &SEQ_SIZE
we get the error:
ORA-32044: cycle detected while executing recursive WITH query
Here’s what the Oracle documentation says about cycles:
If you omit the CYCLE clause, then the recursive WITH clause returns an error if cycles are discovered. In this case, a row forms a cycle if one of its ancestor rows has the same values for all the columns in the column alias list for query_name that are referenced in the WHERE clause of the recursive member.
In this case, the only column in the column alias list that is referenced in the WHERE clause of the recursive member is lev. Also, since lev is incremented by 1 at each iteration, it seems to be impossible for an ancestor row to have the same value, only for sibling rows. Anyway, as intimated in the quote above, there is a CYCLE clause available to handle genuine cycles without an error, by marking a cycle row with a specified value and ceasing to expand that row. We can use it as below:
WITH tree_walk(item_id, lev, tot_price, tot_value, path) AS (
SELECT '0', 0, 0, 0, '' path
FROM DUAL
UNION ALL
SELECT itm.id,
trw.lev + 1,
trw.tot_price + itm.item_price,
trw.tot_value + itm.item_value,
trw.path || itm.id
FROM tree_walk trw
CROSS JOIN items itm
WHERE trw.lev < &SEQ_SIZE
) CYCLE lev SET c TO '*' DEFAULT ' '
SELECT path, tot_price, tot_value, c
FROM tree_walk
WHERE lev = &SEQ_SIZE
ORDER BY 1
This does indeed allow the query to run without error, but the output shows a blank value for the added ‘c’ column, indicating no cycle column was encountered, at least on the final iteration. Perhaps cycles were somehow encountered earlier than the final iteration? We can check for this possibility by omitting the final clause:
WHERE lev = &SEQ_SIZE
As explained in the previous section records from all iterations are returned from a call to a recursive subquery factor, unless explicitly excluded. When we do this we find that still none of the records are marked as cycles (you can check the log file, item_seqs_rsf_cycle.log, in the GitHub project). Strange!
4 Item Sequence Generation by Pure SQL - Paths via Nested Table
↑ Contents
↓ Common Syntax Elements
↓ MP: Multiset Permutation [Items may repeat, order matters]
↓ MC: Multiset Combination [Items may repeat, order does not matter]
↓ SP: Set Permutation [Items may not repeat, order matters]
↓ SC: Set Combination [Items may not repeat, order does not matter]
In this section we show the SQL queries for generating all the item sequences as in the previous section, but this time storing the paths via nested table.
Script on GitHub: app\item_seqs_rsf_nt.sql
Common Syntax Elements
↑ 4 Item Sequence Generation by Pure SQL - Paths via Nested Table
We can define the nested table type like this:
CREATE OR REPLACE TYPE char_nt AS TABLE OF VARCHAR2(4000)
The item sequences are now accumulated via the expression:
trw.path MULTISET UNION char_nt(itm.id)
The main subquery uses ListAgg to join the items together to allow simpler comparison with the earlier queries that accumulate the path as a string. In order to correctly identify the item paths we need an additional grouping field, since now the items are stored as array elements. We could actually use the concatenated path for this purpose, but let’s assume we are trying to avoid this, and instead use a generated unique identifier based on ROWNUM. We can generate a suitable integer like this:
trw.lev * &N_ITEMS + ROWNUM
The path can then be reconstructed in the main subquery using ListAgg, referencing the array within a TABLE operator with CROSS APPLY.
ListAgg(pth.COLUMN_VALUE, '')
...
CROSS APPLY TABLE(trw.path) pth
...
GROUP BY trw.path_uid, trw.tot_price, trw.tot_value
MP: Multiset Permutation [Items may repeat, order matters]
↑ 4 Item Sequence Generation by Pure SQL - Paths via Nested Table
SQL
WITH tree_walk(item_id, lev, tot_price, tot_value, path, path_uid) AS (
SELECT '0', 0, 0, 0, char_nt(), 0
FROM DUAL
UNION ALL
SELECT itm.id,
trw.lev + 1,
trw.tot_price + itm.item_price,
trw.tot_value + itm.item_value,
trw.path MULTISET UNION char_nt(itm.id),
trw.lev * &N_ITEMS + ROWNUM
FROM tree_walk trw
JOIN items itm
ON trw.lev < &SEQ_SIZE
)
SELECT ListAgg(pth.COLUMN_VALUE, '') path,
trw.tot_price, trw.tot_value
FROM tree_walk trw
CROSS APPLY TABLE(trw.path) pth
WHERE lev = &SEQ_SIZE
GROUP BY trw.path_uid, trw.tot_price, trw.tot_value
ORDER BY 1
Join/Where Condition
The join condition is the same as for the string concatenation version.
JOIN items itm
ON trw.lev < &SEQ_SIZE
MC: Multiset Combination [Items may repeat, order does not matter]
↑ 4 Item Sequence Generation by Pure SQL - Paths via Nested Table
SQL
WITH tree_walk(item_id, lev, tot_price, tot_value, path, path_uid) AS (
SELECT '0', 0, 0, 0, char_nt(), 0
FROM DUAL
UNION ALL
SELECT itm.id,
trw.lev + 1,
trw.tot_price + itm.item_price,
trw.tot_value + itm.item_value,
trw.path MULTISET UNION char_nt(itm.id),
trw.lev * &N_ITEMS + ROWNUM
FROM tree_walk trw
JOIN items itm
ON itm.id >= trw.item_id
AND trw.lev < &SEQ_SIZE
)
SELECT ListAgg(pth.COLUMN_VALUE, '') path,
trw.tot_price, trw.tot_value
FROM tree_walk trw
CROSS APPLY TABLE(trw.path) pth
WHERE lev = &SEQ_SIZE
GROUP BY trw.path_uid, trw.tot_price, trw.tot_value
ORDER BY 1
The join condition is the same as for the string concatenation version:
Join/Where Condition
JOIN items itm
ON itm.id >= trw.item_id
AND trw.lev < &SEQ_SIZE
SP: Set Permutation [Items may not repeat, order matters]
↑ 4 Item Sequence Generation by Pure SQL - Paths via Nested Table
SQL
WITH tree_walk(item_id, lev, tot_price, tot_value, path, path_uid) AS (
SELECT '0', 0, 0, 0, char_nt(), 0
FROM DUAL
UNION ALL
SELECT itm.id,
trw.lev + 1,
trw.tot_price + itm.item_price,
trw.tot_value + itm.item_value,
trw.path MULTISET UNION char_nt(itm.id),
trw.lev * &N_ITEMS + ROWNUM
FROM tree_walk trw
JOIN items itm
ON NOT EXISTS (SELECT 1
FROM TABLE(trw.path) pth
WHERE pth.COLUMN_VALUE = itm.id)
WHERE trw.lev < &SEQ_SIZE
) CYCLE lev SET c TO '*' DEFAULT ' '
SELECT ListAgg(pth.COLUMN_VALUE, '') path,
trw.tot_price, trw.tot_value
FROM tree_walk trw
CROSS APPLY TABLE(trw.path) pth
WHERE lev = &SEQ_SIZE
GROUP BY trw.path_uid, trw.tot_price, trw.tot_value
ORDER BY 1
Note that we need to add the CYCLE clause in this case to avoid (see the discussion in the previous section around strange behaviour in this area):
ORA-32044: cycle detected while executing recursive WITH query
Join/Where Condition
We cannot use a simple LIKE condition in the nested table case, but instead we can check that the candidate item does not exist in the array, using the TABLE operator on the array within a NOT EXISTS subquery:
JOIN items itm
ON NOT EXISTS (SELECT 1
FROM TABLE(trw.path) pth
WHERE pth.COLUMN_VALUE = itm.id)
WHERE trw.lev < &SEQ_SIZE
SC: Set Combination [Items may not repeat, order does not matter]
↑ 4 Item Sequence Generation by Pure SQL - Paths via Nested Table
SQL
WITH tree_walk(item_id, lev, tot_price, tot_value, path, path_uid) AS (
SELECT '0', 0, 0, 0, char_nt(), 0
FROM DUAL
UNION ALL
SELECT itm.id,
trw.lev + 1,
trw.tot_price + itm.item_price,
trw.tot_value + itm.item_value,
trw.path MULTISET UNION char_nt(itm.id),
trw.lev * &N_ITEMS + ROWNUM
FROM tree_walk trw
JOIN items itm
ON itm.id > trw.item_id
WHERE trw.lev < &SEQ_SIZE
)
SELECT ListAgg(pth.COLUMN_VALUE, '') path,
trw.tot_price, trw.tot_value
FROM tree_walk trw
CROSS APPLY TABLE(trw.path) pth
WHERE lev = &SEQ_SIZE
GROUP BY trw.path_uid, trw.tot_price, trw.tot_value
ORDER BY 1
The join condition is the same as for the string concatenation version:
Join/Where Condition
JOIN items itm
ON itm.id > trw.item_id
WHERE trw.lev < &SEQ_SIZE
5 Item Sequence Generation by Mixed SQL and PL/SQL
↑ Contents
↓ Recursion vs Iteration
↓ Join Condition Function
↓ Shared Procedures and Function
↓ PL/SQL Recursion
↓ PL/SQL Iteration
Recursion vs Iteration
↑ 5 Item Sequence Generation by Mixed SQL and PL/SQL
In the previous section we showed how recursive SQL can be used to generate item sequences following the approach specified algorithmically in the first article. If we use the procedural language PL/SQL, with embedded SQL, we can also use recursive functions to achieve the same results. In addition we will see that we can generate the sequences without recursion, but using simple iteration in PL/SQL.
When using recursive SQL intermediate paths are stored internally without explicit arrays or tables, but when using PL/SQL as the generative mechanism we need to use either an array or a temporary table (although with recursive function and array, only an array type is needed with results piped from the function).
This gives us an additional four methods to add to our pure SQL method. The two methods using arrays are implemented as pipelined functions that are called directly from a query or view. The two methods using a temporary table are implemented as procedures since a query can’t call a function that writes to a table, with the main query or view then querying the result records in the temporary table.
Script on GitHub: app\item_seqs_pls.sql
Join Condition Function
↑ 5 Item Sequence Generation by Mixed SQL and PL/SQL
We can create a function for the join condition on items being joined to the current paths. We will use this in the queries in this section on small example problems, but will see in a later article that using a function in this way can adversely affect performance.
FUNCTION Seq_Type_Condition_YN(
p_seq_type VARCHAR2,
p_item_id VARCHAR2,
p_item_id_prior VARCHAR2,
p_path VARCHAR2)
RETURN VARCHAR2 IS
l_ret_yn VARCHAR2(1) := 'N';
BEGIN
CASE p_seq_type
WHEN 'MP' THEN
l_ret_yn := 'Y';
WHEN 'MC' THEN
IF p_item_id >= p_item_id_prior THEN l_ret_yn := 'Y'; END IF;
WHEN 'SP' THEN
IF Nvl(p_path,'x') NOT LIKE '%' || p_item_id || '%' THEN l_ret_yn := 'Y'; END IF;
WHEN 'SC' THEN
IF p_item_id > p_item_id_prior THEN l_ret_yn := 'Y'; END IF;
END CASE;
RETURN l_ret_yn;
END Seq_Type_Condition_YN;
Shared Procedures and Function
↑ 5 Item Sequence Generation by Mixed SQL and PL/SQL
↓ Temporary Table Insert Procedures
↓ Array Root Function - initial_Path
Temporary Table Insert Procedures
↑ Shared Procedures and Function
The two temporary table procedures can share two procedures for insertion into the small_paths temporary table:
- insert_Initial_Path: This inserts the (dummy) root record into the temporary table, after deleting any existing records
- insert_Paths: This inserts subsequent records into the temporary table
- Insert, selecting from small_paths
- joining items according to the sequence type, via a call to Seq_Type_Condition_YN
- Delete the prior level records from small_paths
- Insert, selecting from small_paths
PROCEDURE insert_Initial_Path IS
BEGIN
DELETE small_paths;
INSERT INTO small_paths (
path, lev, tot_price, tot_value, item_id
) VALUES ('', 0, 0, 0, '0');
END insert_Initial_Path;
PROCEDURE insert_Paths(
p_seq_type VARCHAR2,
p_lev PLS_INTEGER) IS
BEGIN
INSERT INTO small_paths (
path, lev, tot_price, tot_value, item_id
)
SELECT smp.path || itm.id,
p_lev,
smp.tot_price + itm.item_price,
smp.tot_value + itm.item_value,
itm.id
FROM small_paths smp
JOIN items itm
ON Item_Seqs.Seq_Type_Condition_YN(
p_seq_type => p_seq_type,
p_item_id => itm.id,
p_item_id_prior => smp.item_id,
p_path => smp.path) = 'Y';
DELETE small_paths WHERE lev = p_lev - 1;
END insert_Paths;
Array Root Function - initial_Path
↑ Shared Procedures and Function
The two array functions can share a function that returns the (dummy) root record:
- initial_Path: This returns the (dummy) root record
FUNCTION initial_Path
RETURN small_paths%ROWTYPE IS
l_path_req small_paths%ROWTYPE;
BEGIN
SELECT '', 0, 0, 0, '0' INTO l_path_req FROM DUAL;
RETURN l_path_req;
END initial_Path;
PL/SQL Recursion
↑ 5 Item Sequence Generation by Mixed SQL and PL/SQL
↓ Temporary Table Recursion - Pop_Table_Recurse
↓ Array Recursion - Array_Recurse
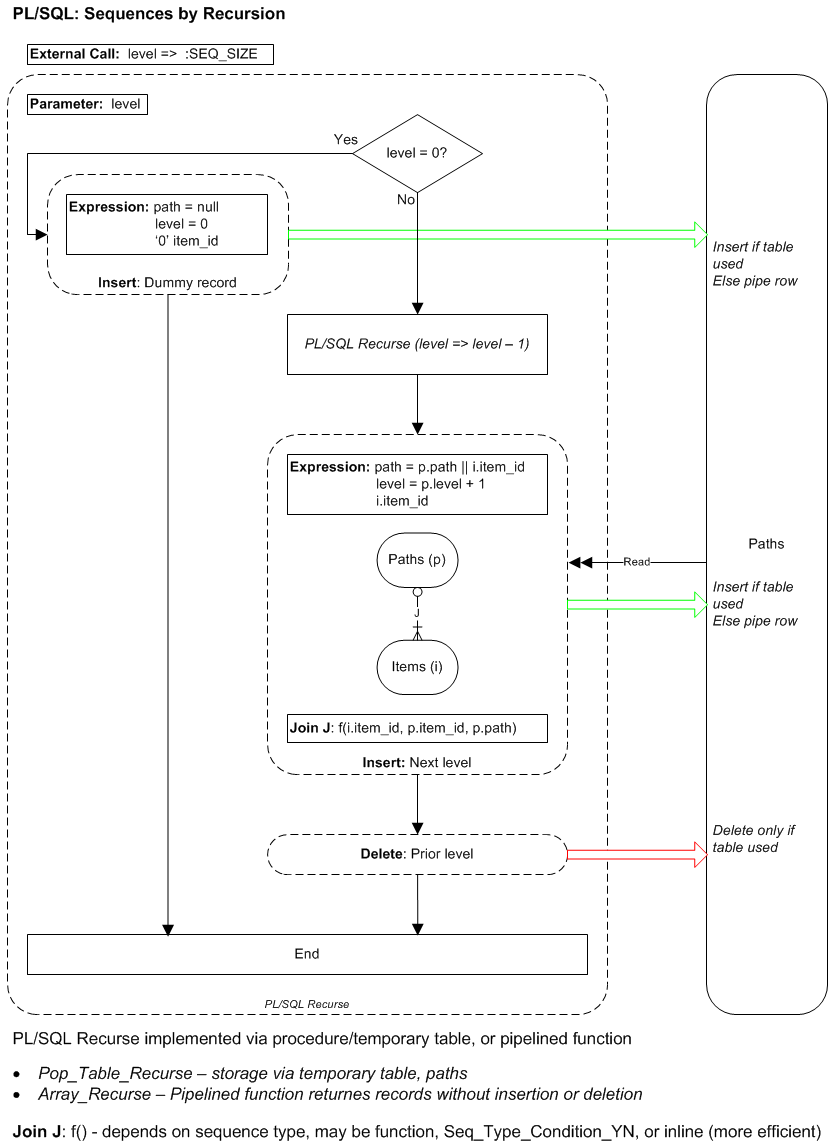
The diagram shows process and data flows for sequence generation by PL/SQL recursion using either array or temporary table for storage of intermediate paths.
Temporary Table Recursion - Pop_Table_Recurse
The temporary table recursion procedure uses the shared insertion procedures.
- If level = 0 then
- Insert (dummy) root record, by calling insert_Initial_Path
- Return
- End if
- Call (recursively) Pop_Table_Recurse passing level - 1
- Insert records at current level, then delete prior level, by calling insert_Paths
PROCEDURE Pop_Table_Recurse(
p_seq_type VARCHAR2,
p_lev PLS_INTEGER := NULL) IS
BEGIN
IF p_lev = 0 THEN
insert_Initial_Path;
RETURN;
END IF;
Pop_Table_Recurse(p_seq_type, Nvl(p_lev, g_seq_size) - 1);
insert_Paths(p_seq_type => p_seq_type,
p_lev => Nvl(p_lev, g_seq_size));
END Pop_Table_Recurse;
Array Recursion - Array_Recurse
The array recursion function uses the shared function initial_Path.
- If level = 0 then
- Pipe (dummy) root record, by calling initial_Path
- Return
- End if
- Loop over query returning the next level paths
- This selects from a recursive call to Array_Recurse. passing level - 1
- joining items according to the sequence type, via a call to Seq_Type_Condition_YN
- Pipe the record
- This selects from a recursive call to Array_Recurse. passing level - 1
- End loop
FUNCTION Array_Recurse(
p_seq_type VARCHAR2,
p_lev PLS_INTEGER := NULL)
RETURN paths_arr PIPELINED IS
BEGIN
IF p_lev = 0 THEN
PIPE ROW(initial_Path);
RETURN;
END IF;
FOR rec IN (
SELECT smp.path || itm.id path,
smp.lev + 1 lev,
smp.tot_price + itm.item_price tot_price,
smp.tot_value + itm.item_value tot_value,
itm.id item_id
FROM Array_Recurse(p_seq_type, Nvl(p_lev, g_seq_size) - 1) smp
JOIN items itm
ON Item_Seqs.Seq_Type_Condition_YN(
p_seq_type => p_seq_type,
p_item_id => itm.id,
p_item_id_prior => smp.item_id,
p_path => smp.path) = 'Y') LOOP
PIPE ROW(rec);
END LOOP;
END Array_Recurse;
Note that, although we need to define an array type, paths_arr, and make it the return type of the function, we do not need to declare any array instances explicitly.
PL/SQL Iteration
↑ 5 Item Sequence Generation by Mixed SQL and PL/SQL
↓ Temporary Table Iteration - Pop_Table_Iterate
↓ Array Iteration - Array_Iterate
The diagram shows process and data flows for sequence generation by PL/SQL iteration using either array or table for storage of intermediate paths.
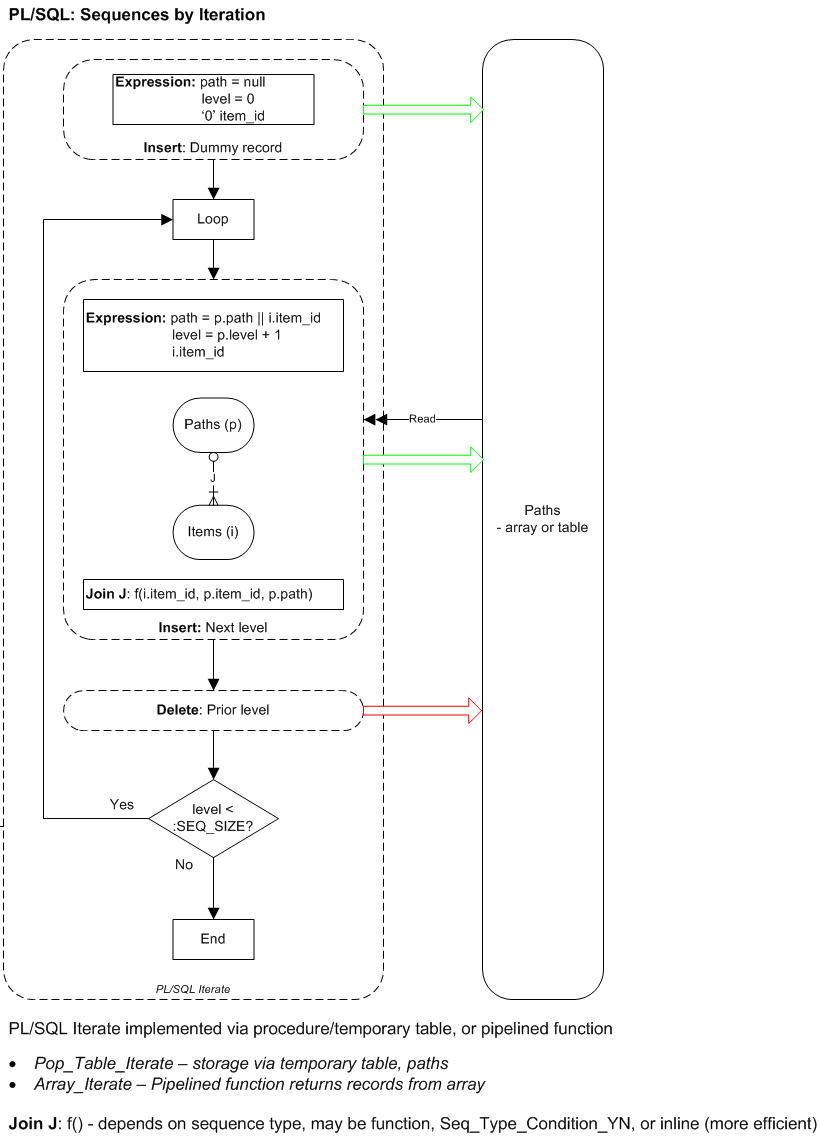
Temporary Table Iteration - Pop_Table_Iterate
The temporary table iteration procedure uses the shared insertion procedures.
- Insert (dummy) root record, by calling insert_Initial_Path
- Loop from 1 to :SEQ_SIZE
- Insert records at current level, then delete prior level, by calling insert_Paths
- End loop
PROCEDURE Pop_Table_Iterate(
p_seq_type VARCHAR2) IS
BEGIN
insert_initial_Path;
FOR i IN 1..g_seq_size LOOP
insert_Paths(p_seq_type => p_seq_type,
p_lev => i);
END LOOP;
END Pop_Table_Iterate;
Array Iteration - Array_Iterate
The array iteration function uses the shared function initial_Path.
- Declare arrays for paths and new paths
- Initialize paths array with (dummy) root record, by calling initial_Path
- Loop from 1 to :SEQ_SIZE
- Select into the new paths array:
- driving from the paths array
- joining items according to the sequence type, via a call to Seq_Type_Condition_YN
- This selects from a recursive call to Array_Recurse. passing level - 1
- Set the paths array equal to the new paths array
- Select into the new paths array:
- End loop
- Loop over the paths array
- Pipe the record
- End loop
FUNCTION Array_Iterate(
p_seq_type VARCHAR2)
RETURN paths_arr PIPELINED IS
l_paths_lis paths_arr := paths_arr(initial_Path);
l_paths_new_lis paths_arr;
BEGIN
FOR i IN 1..g_seq_size LOOP
SELECT smp.path || itm.id,
smp.lev + 1,
smp.tot_price + itm.item_price,
smp.tot_value + itm.item_value,
itm.id
BULK COLLECT INTO l_paths_new_lis
FROM TABLE(l_paths_lis) smp
JOIN items itm
ON Item_Seqs.Seq_Type_Condition_YN(
p_seq_type => p_seq_type,
p_item_id => itm.id,
p_item_id_prior => smp.item_id,
p_path => smp.path) = 'Y';
l_paths_lis := l_paths_new_lis;
END LOOP;
FOR i IN 1..l_paths_lis.COUNT LOOP
PIPE ROW(l_paths_lis(i));
END LOOP;
END Array_Iterate;
Note that, in order to collect a new set of records into an array based on the prior set, we need to define two arrays and move the new set to the current array after each iteration.
6 Conclusion
In the first article we showed in an abstract way how recursive techniques may be used to generate sequences of items that can form the basis of solutions for larger problems involving constraints and value optimization.
In this article we demonstrated how these algorithms can be implemented using recursive SQL. We also demonstrated how PL/SQL can be used to implement both recursive and iterative versions with embedded SQL, using either temporary tables or arrays for path storage.
In the next article we will extend consideration beyond just the generation of sequences to optimization problems where we want to select sequences that maximize a value measure subject to constraints. This will follow a mathematical approach similar to the first article for similar reasons.